Force Applied to Masses Suspended by Springs: Find Displacements

[sam12345]

Homework Statement

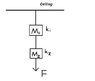
A pair of masses M1, M2 is suspended vertically by a pair of spring, with spring constant k1, k2. ( see the attachment for the picture)

a.A downward force F is applied to bottom mass. Find the downward displacements d1 and d 2 of the equilibrium positions of the Mass M1and M2 due to the force. Note that effect of gravity is already taken into account in determing the equilibrium positions.


b.At time t =0, the downward force is removed. What are the equation of motion and initial conditions that determine the displacements d1(t) and d2(t) for t greater than 0? You need not solve the equations.

Homework Equations

m₂g=k₂x₂
k₂x₂ + m₂g+ m₁g=k₁x₁
then i added them, I get 2m₂g +m₁g=k₁x₁

F=-kx

The Attempt at a Solution

m₂g=k₂x₂
k₂x₂ + m₂g+ m₁g=k₁x₁
then i added them, I get 2m₂g +m₁g=k₁x₁.
after this, I have no idea how to solve this! please help!

 

[sam12345]

Btw, this is a Caltech problem!

 

[jhae2.718]

For A, try creating separate free body diagrams for $m_1$ and $m_2$ and finding $\Sigma F_y=F_{app}$. Then, solve each for $d_1$ and $d_2$.

 

[Jebus_Chris]

a) Both springs will experience force F. Since they are already in equilibrium you can "ignore" the masses.
$$F=k_1d_1$$
$$F=k_2d_2$$
b) Simple SHM equations.