- #1
Ikastun
- 10
- 0
Two identical triangles are placed inside a water tank as shown in the diagram below. The triangles are fixed in position. On which triangle will a greater force be exerted?
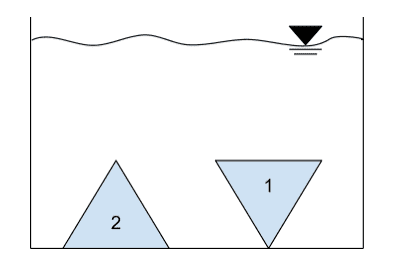
1
2
Equal on both.
Cannot say
The question is part of a mechanical aptitude test. The correct answer is 2, but there is no explanation.
I do not understand why is 2, and not "equal on both". Can anyone give me some clues?.