Chris42163
- 6
- 0
I'm building an excel dragstrip model. I already have a working model that incorporates force exerted at the rear tires, force of drag, and force of rolling resistance. Now, I want to take into account the linear force that acts on the front tires that is required to accelerate them. There is both a linear component and an angular component. The linear component is already accounted for, because the mass of the wheel, tire, brakes, and spindle are included in the overall mass of the car. The angular inertia of these components is not accounted for.
I am not a regular here, and am not good at typing stuff out. I did some beer math and a free body diagram, and am surprised at the result. I have never seen it calculated this way, and have searched google all day to no avail. Please confirm or shoot down my work. Thanks!
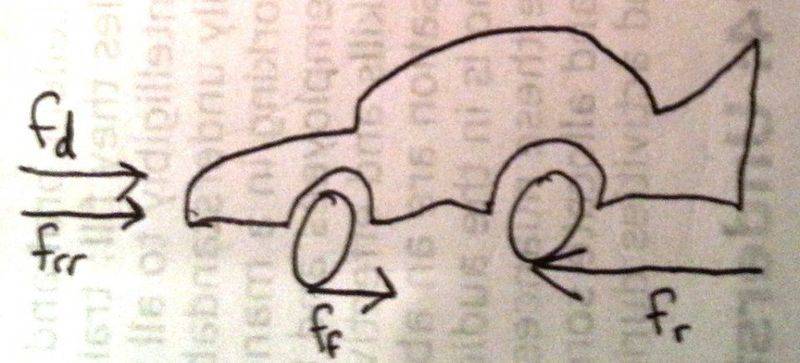
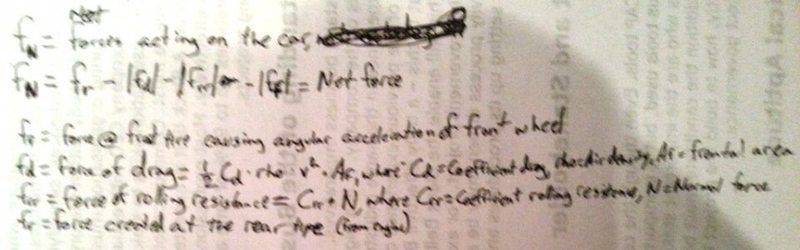
All of the other forces are independent of angular acceleration, but the force at the front wheels, "ff," must be calculated as part of the acceleration equation.
equation 1:
fnet=mc*a, where mc is the mass of the entire car, and a is the total acceleration of the car
equation 2:
fnet=fr-fd-frr-ff, where the forces are defined above, and I prefer to use the absolute value of the forces, but I couldn't find the abs val symbol. So I will treat all forces with positive values that should be subtracted if they act against thrust, or fr.
equation 3:
torque = Iα
equation 4:
Also, torque = ff*rf, where rf is the radius of the front tire and ff is the linear force applied at the front tire.
equation 5:
I=moment of inertia of the wheel, which =mf*ri2, where mf is the mass of the front wheel, tire, brake rotor, spindle, and ri is the effective inertial radius
ri is going to be some radius between the axis of rotation and rf where, for the purposes of calculating the moment of inertia, all the mass of the rotating assembly could be concentrated to a single radius. Therefore, equation 6: ri=rf*Ci, where Ci is some coefficient between 0 and 1 that represents the percentage of the distance. substituting that back into the equation for I, above:
equation 7:
I=mf*rf2*Ci2
equation 8:
α=angular acceleration, which = a/rf, where a is the linear acceleration of the car. α is given in rad/s
I've worked out things to substitute for torque, I, and α. So,
equation 9
(ff*rf)=(mf*ri2)*(a/rf)
substituting equation 6 for ri into equation 9, we get
equation 10
(ff*rf)=(mf*rf2*Ci2)*(a/rf)
Simplifying:
ff=(mf*rf2*Ci2*a)/rf2
cancel like terms:
ff=mf*Ci2*a
Now for ff, plug equation 10 into equation 2
equation 11
fnet=fr-fd-frr-(mf*Ci2*a)
For fnet, substitute equation 1 to get:
equation 12
mc*a=fr-fd-frr-(mf*Ci2*a)
now solve for a:
(mc*a)+(mf*Ci2*a)=fr-fd-frr
a*(mc+mf*Ci2)=fr-fd-frr
and finally:
a=(fr-fd-frr)/(mc+mf*Ci2)
If I've done this correctly, I have all of the values on the right hand side of the equation in my model and can solve for a. It didn't make as big a difference in the model as I expected, and I was surprised by the cancellation of rf in equation 10, because it means that the radius of the front tire doesn't actually matter, only the ratio between the radius and the effective inertial radius, ri.
Thanks for any insight or corrections.
I am not a regular here, and am not good at typing stuff out. I did some beer math and a free body diagram, and am surprised at the result. I have never seen it calculated this way, and have searched google all day to no avail. Please confirm or shoot down my work. Thanks!
All of the other forces are independent of angular acceleration, but the force at the front wheels, "ff," must be calculated as part of the acceleration equation.
equation 1:
fnet=mc*a, where mc is the mass of the entire car, and a is the total acceleration of the car
equation 2:
fnet=fr-fd-frr-ff, where the forces are defined above, and I prefer to use the absolute value of the forces, but I couldn't find the abs val symbol. So I will treat all forces with positive values that should be subtracted if they act against thrust, or fr.
equation 3:
torque = Iα
equation 4:
Also, torque = ff*rf, where rf is the radius of the front tire and ff is the linear force applied at the front tire.
equation 5:
I=moment of inertia of the wheel, which =mf*ri2, where mf is the mass of the front wheel, tire, brake rotor, spindle, and ri is the effective inertial radius
ri is going to be some radius between the axis of rotation and rf where, for the purposes of calculating the moment of inertia, all the mass of the rotating assembly could be concentrated to a single radius. Therefore, equation 6: ri=rf*Ci, where Ci is some coefficient between 0 and 1 that represents the percentage of the distance. substituting that back into the equation for I, above:
equation 7:
I=mf*rf2*Ci2
equation 8:
α=angular acceleration, which = a/rf, where a is the linear acceleration of the car. α is given in rad/s
I've worked out things to substitute for torque, I, and α. So,
equation 9
(ff*rf)=(mf*ri2)*(a/rf)
substituting equation 6 for ri into equation 9, we get
equation 10
(ff*rf)=(mf*rf2*Ci2)*(a/rf)
Simplifying:
ff=(mf*rf2*Ci2*a)/rf2
cancel like terms:
ff=mf*Ci2*a
Now for ff, plug equation 10 into equation 2
equation 11
fnet=fr-fd-frr-(mf*Ci2*a)
For fnet, substitute equation 1 to get:
equation 12
mc*a=fr-fd-frr-(mf*Ci2*a)
now solve for a:
(mc*a)+(mf*Ci2*a)=fr-fd-frr
a*(mc+mf*Ci2)=fr-fd-frr
and finally:
a=(fr-fd-frr)/(mc+mf*Ci2)
If I've done this correctly, I have all of the values on the right hand side of the equation in my model and can solve for a. It didn't make as big a difference in the model as I expected, and I was surprised by the cancellation of rf in equation 10, because it means that the radius of the front tire doesn't actually matter, only the ratio between the radius and the effective inertial radius, ri.
Thanks for any insight or corrections.
