meggs521
- 9
- 0
Hey guys, I've been reading threads on here for a little bit and now I have a question I need some help with. I tried doing a search, but I didn't really know what I was looking for so it wasn't too successful. But here it is:
My boss gave me this question to figure out and I'm not really sure where to start. I'm interning with an engineering firm and the following question arose.
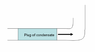
If we have an 8" Steam pipe that has steam at 80 psia and some of the steam condenses within the pipe forming a "plug of condensate" about 10' long, how much force will be applied on the end of the pipe if it goes into a 90 degree turn with a short radius?
The velocities I'm supposed to check this for are 4000 fpm, 6000 fpm, and 10000 fpm. I'm currently a sophomore in engineering, so I don't know too much about how to do this. Of course F=ma and all that, but without the acceleration I'm kind of lost.
I also know that in an 8" pipe the mass of water is approximately 21 lbs/ ft, so at 10' there's roughly 210 lbs of water. What sort of equation or method should I be using?
Any help would be very helpful as I'm pretty lost. Here's a picture of the pipe in case my description wasn't good enough.
Thanks again!
~Meg
I also have two alternatives to the 90 degree bend. One is a 45 degree slant and the other simply has the pipe end with a blind flange. I've attached pictures of each of these as well.
Would I solve these two the same way as the above problem?
My boss gave me this question to figure out and I'm not really sure where to start. I'm interning with an engineering firm and the following question arose.
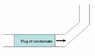
If we have an 8" Steam pipe that has steam at 80 psia and some of the steam condenses within the pipe forming a "plug of condensate" about 10' long, how much force will be applied on the end of the pipe if it goes into a 90 degree turn with a short radius?
The velocities I'm supposed to check this for are 4000 fpm, 6000 fpm, and 10000 fpm. I'm currently a sophomore in engineering, so I don't know too much about how to do this. Of course F=ma and all that, but without the acceleration I'm kind of lost.
I also know that in an 8" pipe the mass of water is approximately 21 lbs/ ft, so at 10' there's roughly 210 lbs of water. What sort of equation or method should I be using?
Any help would be very helpful as I'm pretty lost. Here's a picture of the pipe in case my description wasn't good enough.
Thanks again!
~Meg
I also have two alternatives to the 90 degree bend. One is a 45 degree slant and the other simply has the pipe end with a blind flange. I've attached pictures of each of these as well.
Would I solve these two the same way as the above problem?