Baxidur
- 8
- 0
Hi
Finding it hard to find exact information on the maths and forces behind this on the internet, (maybe my search terms to blade)
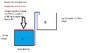
If I have a 10cm diamter cylinder that's 10cm deep and filled with water and a piston (weightless piston for the example) at the top and a 1 cm diameter pipe running from the base, how much weight would I have to place on the piston to push all of the water 20cm high into another recepticle?
Thanks in advance for anyone that can answer this, Also the formulas required to calculate it would be great
Baxidur
Finding it hard to find exact information on the maths and forces behind this on the internet, (maybe my search terms to blade)
If I have a 10cm diamter cylinder that's 10cm deep and filled with water and a piston (weightless piston for the example) at the top and a 1 cm diameter pipe running from the base, how much weight would I have to place on the piston to push all of the water 20cm high into another recepticle?
Thanks in advance for anyone that can answer this, Also the formulas required to calculate it would be great
Baxidur