masterchiefo
- 211
- 2
Homework Statement
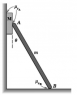
A block of mass M = 1 kg is placed between a vertical wall and the end of A
beam mass m = 10 kg . If μ S = 0.6 A , determine the minimum value of the angle θ min
θ for which the block remains in equilibrium and the coefficient of friction
Static B μ S corresponding to prevent the beam from sliding B.
Picture of the problem in attachment.
Homework Equations
The Attempt at a Solution
Block:
∑Fy = +fsablock -Wblock = 0
∑Fx = +Nblock = 0
Beam:
∑Fx = -fsabeam + NA =0
∑Fy = -Wbeam +NB + fsabeam =0
is this correct? and how can I possibly find the min θ?
thank you.
Attachments
Last edited: