Forces On a Moving Train Traveling Around a Curve

[tomtomtom1]

TL;DR Summary

Forces Involved Of A Moving Train Travelling Around A Curve

Hello all

I am trying to work out the forces involved of a moving train around a curve traveling at a constant speed.

I have the following:-

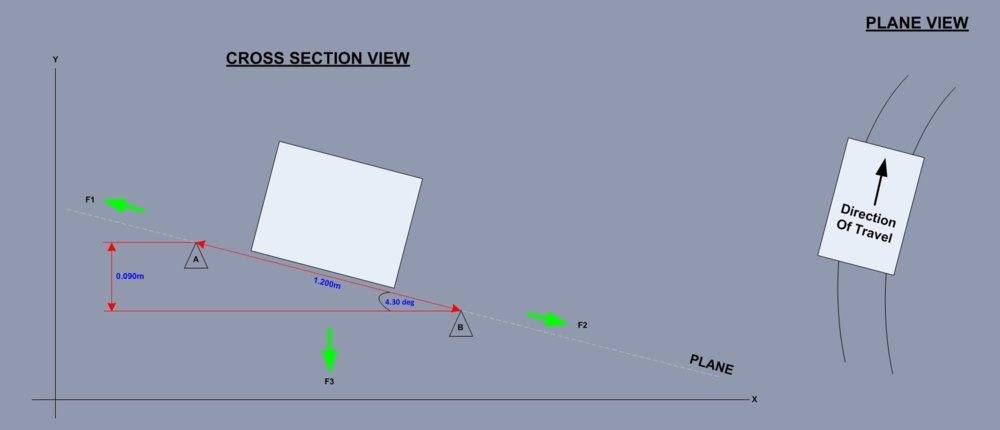
The image on the left is a cross section of a train traveling around a curve, you can think of the train moving away from you.

The image on the right in the same train but in plane view but illustrates the radius.

I am trying to work out the Forces F1, F2 and F3.

I know the following:-

- Speed = 200mph

- Weight = 101605kg

- Radius = 500m

- Gravity = 9.81m/s^2

- Distance between Rails = 1.2m

- Height Difference between Rail A and Rail B = 0.090m

- Angle = 4.30 deg

The first thing that I tried to do was to convert the train weight of 101605 kg into a Mass by dividing by 9.81 m/s^2, however I ended up with some strange units:-

101605kg / 9.81m/s^2 = 10357.28848 (kg s^2)/m - ??

The reason why I wanted to find the Mass was because I wanted to use the F = MA equation to work out Force in Newtons.

Because I didn't get far with this I tried to convert the speed of the train which is 200mph into an acceleration but since the train is traveling around the curve at a constant speed of 200mph there is no acceleration which I am struggling to come to terms with.

Can I ask how would the Forces F1 F2 and F3 be worked out?

Can anyone point me in the right direction?

Thank you.

 

[BvU]

Weight = 101605 kg

Do you mean mass = 101605 kg ? The kilogram is a unit of mass.

constant speed of 200mph there is no acceleration

There is: the velocity of the train changes. Not in magnitude but in direction.

For a circular motion a centripetal force is needed. Can you find out how big it has to be in this case ?

[edit]
200 mph is a disaster speed for a curve radius of 500 m

 

[cjl]

[edit]
200 mph is a disaster speed for a curve radius of 500 m

It's not entirely unreasonable if the train is a roller coaster...

 

[BvU]

200 mph, 500 m -- not a roller coaster

 

[cjl]

I know, I was being a bit facetious (though the fastest roller coaster is 150mph, so that's not that far off). That would be just about a 2G curve though, so it would be pretty ridiculous (and it would require 60 degree banking).

EDIT: Maybe it's 5km? That bank angle from OP's diagram is still not quite enough even in that case, but it at least seems to kind of work out as reasonable...

 

[hutchphd]

I don't see the position of the center of mass of the car noted anywhere. That will of course determine the actual disaster speed.

 

[osilmag]

F3 would be the weight multiplied by the cosine of the incline.