plumeria28
- 4
- 0
Homework Statement
Two forces act on a 4.00 kg mass which is sitting at rest on a horizontal frictionless surface. One force is 6.50 N directed 55° West of South, the other is 7.00 N directed 25° North of West. What acceleration does the mass receive?
Homework Equations
sin = o/h
cos = a/h
tan = o/a
a = F/m
The Attempt at a Solution
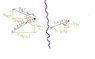
I drew forces (not accurately) on paint (attachment) to help me solve this question then did the following calculations:
Fapx1
sin = o/h sin35° = o/6.5N o = 3.7N
Fapx2
sin = o/h sin25° = o/7N o = 3N [N]
Fapx = Fapx1 + Fapx2
Fapx = 3.7N - 3N
Fapx = 0.7N
Fapy1
cos = a/h cos35° = a/6.5N a = 5.3N [W]
Fapy2
cos = a/h cos25° = a/7N a = 6.3N [W]
Fapy = Fapy1 + Fapy2
Fapy = 5.3N + 6.3N
Fapy = 11.6N
************************************************
tan = o/a tan = 11.6/0.7 tan = 86.5°
sin = o/h sin86.5° = 11.6/h h = 11.622N
************************************************
a = F/m a = 11.622N/4.00kg a = 2.9 m/s^2
_____________________________________________________________________________
I was wondering if I did the question right. Did I get the right answer?