Formal proof of Thevenin theorem

[cianfa72]

TL;DR

Formal proof of Thevenin theorem from an algebraic point of view

Hi,
I am looking for a formal proof of Thevenin theorem. Actually the first point to clarify is why any linear network seen from a port is equivalent to a linear bipole.

In other words look at the following picture: each of the two parts are networks of bipoles themselves.

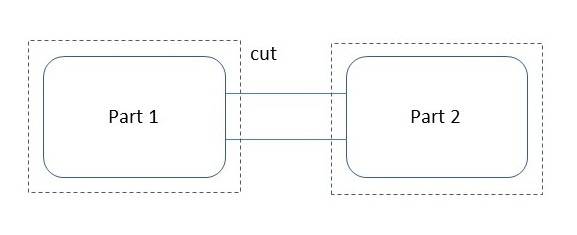
Why the part 1 -- as seen from the interconnection's port (topological cut) -- is equivalent to a linear bipole itself ?

Thank you.

 

[DaveE]

Have you tried a google search? I did "proof of thevenin's theorem pdf" and got so much good stuff I honestly don't know which one to link to here. Many have references to other papers too.

 

[cianfa72]

Have you tried a google search? I did "proof of thevenin's theorem pdf" and got so much good stuff I honestly don't know which one to link to here.

Yes, I believe the point is to show - from a linear algebraic point of view - that the linear system of the complete composite network actually breaks in two parts: by mean of elimination (e.g. Gauss elimination) we may always reduce each part to a linear equation (the Thevenin or Norton equivalent).

 

[cianfa72]

@Delta Prime can you prove it ?

 

[jim mcnamara]

@cianfa72 did you mean to post this in another thread? As it stands now, this makes no sense.

 

[cianfa72]

@cianfa72 did you mean to post this in another thread?

No, I mean whether or not you can confirm my argument about the structure of the linear system and how to break it in the two parts involved.

 

[jim mcnamara]

Thanks for the clarity.