- #1
Sharya19
- 21
- 0
Hello again. Having some issues on Fourier transform. Can someone please tell me how to proceed? Need to solve this then use some software to check my answer but how to solve for a and b. Plzz help
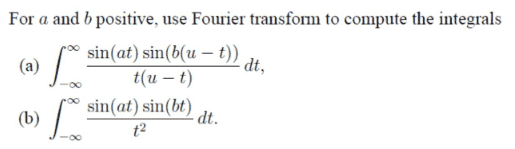
ok thnks. will tryKlaas van Aarsen said:Hint for (a): the integral has the form of a convolution $g(u) \star h(u)$. So we can apply the convolution theorem, evaluate $G(f)\cdot H(f)$, and take its inverse Fourier transform.
We can pick for instance $g(u)=\frac{\sin(au)}{au}$ and $h(u)=\frac{\sin(bu)}{bu}$. And look up their Fourier transforms in a table.
Hello. i know its simple english u've written but am still not understanding... Sorry... Could u elaborate more? PlzzzzKlaas van Aarsen said:Hint for (a): the integral has the form of a convolution $g(u) \star h(u)$. So we can apply the convolution theorem, evaluate $G(f)\cdot H(f)$, and take its inverse Fourier transform.
We can pick for instance $g(u)=\frac{\sin(au)}{au}$ and $h(u)=\frac{\sin(bu)}{bu}$. And look up their Fourier transforms in a table.
Thnks a lot. as for the Fourier transform table i only have these 2 that my former lecturer left me. As for the definition, can't find any... can any definition be used as I will need to input on Matlab to see if the results corresponds?Klaas van Aarsen said:The convolution $(g\star h)(x)$ is defined as:
$$(g\star h)(x) = \int_{-\infty}^\infty g(t)h(x-t)\,dt$$
And according to the convolution theorem we have:
$$\mathscr F_x\{(g\star h)(x)\}(f)=G(f)H(f)$$
where $G(f)$ is the Fourier transform of $g(x)$, $H(f)$ is the Fourier transform of $h(x)$, and $\mathscr F_x$ is the Fourier transform with respect to the variable $x$.
Put otherwise, we have:
$$(g\star h)(x) = \mathscr F_f^{-1}\{G(f)H(f)\}(x) \tag 1$$
where $\mathscr F_f^{-1}$ is the inverse Fourier transform with respect to the variable $f$
Now let's define $g(x)=\frac{\sin(ax)}{ax}$ and $h(x)=\frac{\sin(bx)}{bx}$.
Then:
$$\int_{-\infty} \frac{\sin(at)\sin(b(u-t))}{t(u-t)}\,dt = ab \int_{-\infty} \frac{\sin(at)}{at}\cdot\frac{\sin(b(u-t))}{b(u-t)}\,dt = ab \int_{-\infty} g(t)h(u-t)\,dt =ab\cdot (g \star h)(u)
= ab\cdot \mathscr F_f^{-1}\{G(f)H(f)\}(u) \tag 2$$
Before we go any further, can you clarify which version of the Fourier transform you have?
That's because there are many different versions around, and they result in different transformations with different variables.
You should have a definition like:
$$\mathscr F_x\{f(x)\}(f) = \int_{-\infty}^\infty f(x)e^{2\pi i f x}\,dx$$
Can you quote the definition that you have that is probably slightly different?
Additionally, we need the Fourier transform of $\frac{\sin{x}}{x}$ or something similar.
Do you have a table of Fourier transforms where you can look it up?
If so, what is the transform you have?
Klaas van Aarsen said:You seem to be missing the actual definition, and you're also missing a table of transforms of common functions.
Anyway, we can refer to the Tables of important Fourier transforms on wiki.
I guess we can pick the version that transforms $f(x)$ to $\hat f(\omega)$ in those tables.
You'll see that the second table on wiki has:
$$\operatorname{sinc}(ax) \longleftrightarrow \frac 1{|a|}\operatorname{rect}\frac{\omega}{2\pi a}$$
where $\operatorname{sync}(x)\overset{\text{def}}=\frac{\sin\pi x}{\pi x}$, and $\operatorname{rect}(x)\overset{\text{def}}=\begin{cases}1&\text{if }-\frac 12< x <\frac 12\\0&\text{otherwise}\end{cases}$.
Can we find the Fourier transform of $\frac{\sin(bx)}{bx}$ with this information?
Sharya19 said:for sin (bx)/bx = 1/|b| rect ω/2πb. is it correct?
fourier function matches the version we picked in my previous post.ok so can we pleasez proceed using the version in your previous post. Am extremely sorry for the wrong answer... am really using my brain(which i think is faultyKlaas van Aarsen said:I'm afraid not.
Note that the definition of $\operatorname{sync}$ contains $\pi$, for which we have to compensate.
To be clear, there are also different versions of $\operatorname{sync}$ around, so we have to be careful. But the version we have here has $\pi$ in it.
We should substitute $a=\frac{b}{\pi}$ so that we get $\operatorname{sync}(ax)=\frac{\sin(\pi ax)}{\pi ax}=\frac{\sin(\pi \frac b\pi x)}{\pi \frac b\pi x}=\frac{\sin(bx)}{bx}$.Btw, you mentioned Matlab.
Note that Matlab has this definition of the Fourier transform.
Matlab'sfourierfunction matches the version we picked in my previous post.
No worries. Careful substitution is a skill that is not trivial.Sharya19 said:ok so can we pleasez proceed using the version in your previous post. Am extremely sorry for the wrong answer... am really using my brain(which i think is faultywhen it comes to maths)
Sharya19 said:ok so can we pleasez proceed using the version in your previous post. Am extremely sorry for the wrong answer... am really using my brain(which i think is faultywhen it comes to maths)
Klaas van Aarsen said:No worries. Careful substitution is a skill that is not trivial.
Anyway, substituting $a=\frac b\pi$ or $b=\pi a$, we get:
$$\frac{\sin(bx)}{bx} = \frac{\sin(\pi ax)}{\pi ax} = \operatorname{sinc}(ax) \longleftrightarrow \frac 1{|a|}\operatorname{rect}\left(\frac\omega{2\pi a}\right)
= \frac 1{|\frac b\pi|}\operatorname{rect}\left(\frac\omega{2\pi \frac b\pi}\right) = \frac\pi{|b|}\operatorname{rect}\left(\frac\omega{2 b}\right)$$
To summarize, we have:
$$\begin{cases}g(x)=\frac{\sin(ax)}{ax} \\ h(x)=\frac{\sin(bx)}{bx} \end{cases} \longleftrightarrow
\begin{cases}G(\omega)=\frac\pi{|a|}\operatorname{rect}\left(\frac\omega{2 a}\right) \\ H(\omega)=\frac\pi{|b|}\operatorname{rect}\left(\frac\omega{2 b}\right) \end{cases}\tag 4$$
Can we tell what $G(\omega)H(\omega)$ is?
And can we substitute everything in formula $(2)$ in my previous https://mathhelpboards.com/threads/fourier-transform.28946/post-127174?
Sharya19 said:G(ω)H(ω) = [π/|a| rect (ω/2a)]*[ π/|b| rect (ω/2b)]
Formula 2 : ab⋅F−1 f {G(f)H(f)}(u) = ab. F-1 f {[π/|a| rect (ω/2a)]*[ π/|b| rect (ω/2b)]} (u) is it correct?
i'm sure we can but how to simplify as there's rect (x) = 1 but we have rect (w/2b), there's no x??Klaas van Aarsen said:Yes.
Can we simplify $G(\omega)H(\omega)$ taking into account that $\operatorname{rect}(x)\overset{\text{def}}=\begin{cases}1&\text{if }-\frac 12< x <\frac 12\\0&\text{otherwise}\end{cases}$?
We need to substitute $x=\frac\omega{2b}$.Sharya19 said:i'm sure we can but how to simplify as there's rect (x) = 1 but we have rect (w/2b), there's no x??
so G(x)H(x) simplified becomes [π/|a|]*[ π/|b|] as rect (a)=rect (b) = 1 for a and b positiveKlaas van Aarsen said:We need to substitute $x=\frac\omega{2b}$.
Then we find that if $-\frac 12 < \frac\omega{2b} <\frac 12$ then $\operatorname{rect}\left(\frac\omega{2b}\right)=1$, and otherwise it is $0$.
Since we know that $b$ is positive, it means that if $-b < \omega <b$ then $\operatorname{rect}\left(\frac\omega{2b}\right)=1$, and otherwise $0$.
That parameter is $\omega$ instead of $x$ and the result depends on its value.Sharya19 said:so G(x)H(x) simplified becomes [π/|a|]*[ π/|b|] as rect (a)=rect (b) = 1 for a and b positive
we use this formula ab⋅F−1 f {G(f)H(f)}(u) = ab. F-1 f {[π/|a|]*[ π/|b|]} (u)... How?Klaas van Aarsen said:That parameter is $\omega$ instead of $x$ and the result depends on its value.
Also note that it is given that both $a$ and $b$ are positive.
So more specifically we have:
$$G(\omega)H(\omega) = \begin{cases}\frac \pi a\cdot \frac \pi b &\text{if } -a<\omega<a \land -b<\omega<b \\ 0 &\text{otherwise}\end{cases}$$
This is again a rectangle function.
So we can use the same transformation pair as before to apply the inverse Fourier transform.
Sharya19 said:we use this formula ab⋅F−1 f {G(f)H(f)}(u) = ab. F-1 f {[π/|a|]*[ π/|b|]} (u)... How?
is this πsinmu/u the answer?Klaas van Aarsen said:Let $m$ be the minimum of the positive $a$ and $b$.
Then we can write $G(\omega)H(\omega)=\frac\pi a\frac\pi b \operatorname{rect}\left(\frac\omega{2m}\right)$.
We have the transformation pair $\frac{\sin{mx}}{mx} \longleftrightarrow \frac\pi {|m|}\operatorname{rect}\left(\frac\omega{2m}\right)$.
Therefore $\mathscr F_\omega^{-1}\{G(\omega)H(\omega)\}(u) = \frac\pi a\frac\pi b\frac m\pi \frac{\sin mu}{mu}$.
So the original integral is $ab\cdot\frac\pi a\frac\pi b\frac m\pi \frac{\sin mu}{mu}=\frac{\pi\sin mu}{u}$ where $m=\min(a,b)$.
Sharya19 said:is this πsinmu/u the answer?
Are there more steps? Need to attend work(will finish at 0500am, won't be able to clarify/answer u if i have any issues concerning the next step if any. Sorry for taking up ur time on a saturday but when it comes to maths well i try i really really try but ...Plzz be online tomorrow to help me again...
Thanks a lot for the help... Am having an issue on Matlab can u help?? The answer am getting is cos at - bt... can u help please?Klaas van Aarsen said:Yes. That is the answer for (a). There are no more steps.
As for (b), hint: substitute $u=0$ in the result of (a).
What did you evaluate?Sharya19 said:Thanks a lot for the help... Am having an issue on Matlab can u help?? The answer am getting is cos at - bt... can u help please?
checking some vids on u tubeKlaas van Aarsen said:What did you evaluate?
syms a b u t
assume(a > 0)
f = sin(a*t)/t
f_FT = fourier(f)
f_FT =g = sinc(a*t/pi)
g_FT = fourier(g)
g_FT =ok thnks will re try it. Thanks a lot for the help. God Bless youKlaas van Aarsen said:Note that the result should be a function of $u$.
Btw, I don't have Matlab myself.
Instead I have access to the opensource Octave, which is identical, except that it doesn't have the symbolic version of the Fourier function that Matlab has...
It does look as if you can use MatLab to do the Fourier transforms that we did by hand.
That is, following the examples given, something like:
will likely work and should show the rectangle function we found.Matlab:syms a b u t assume(a > 0) f = sin(a*t)/t f_FT = fourier(f) f_FT =
Moreover, I see MatLab also has the sinc function, that has the same definition as the one we used. That is, it includes $\pi$.
So we should also be able to do:
If the previous version did not work to find a "clean" rectangle function, this one might.Matlab:g = sinc(a*t/pi) g_FT = fourier(g) g_FT =
Thanks a lot for ur help. Wll try it again. Really Really thankful for ur help. God Bless YOU, UR PARENTS AND UR FAMILY. Thanks a lot lot lot lot lot lotKlaas van Aarsen said:Note that the result should be a function of $u$.
Btw, I don't have Matlab myself.
Instead I have access to the opensource Octave, which is identical, except that it doesn't have the symbolic version of the Fourier function that Matlab has...
It does look as if you can use MatLab to do the Fourier transforms that we did by hand.
That is, following the examples given, something like:
will likely work and should show the rectangle function we found.Matlab:syms a b u t assume(a > 0) f = sin(a*t)/t f_FT = fourier(f) f_FT =
Moreover, I see MatLab also has the sinc function, that has the same definition as the one we used. That is, it includes $\pi$.
So we should also be able to do:
If the previous version did not work to find a "clean" rectangle function, this one might.Matlab:g = sinc(a*t/pi) g_FT = fourier(g) g_FT =
The Fourier Transform is a mathematical tool used to decompose a complex signal into its individual frequency components. It is important because it allows us to analyze and understand complex signals, such as audio and images, in terms of their underlying frequencies.
To solve for a and b in a Fourier Transform, you need to use the formula: a = (1/T) * integral of x(t) * cos(2*pi*f*t) dt and b = (1/T) * integral of x(t) * sin(2*pi*f*t) dt, where T is the period of the signal, x(t) is the signal, and f is the frequency. You will need to use calculus to evaluate the integrals.
Some common issues that arise when solving for a and b in a Fourier Transform include improper selection of the period T, incorrect application of the formula, and errors in evaluating the integrals. It is important to carefully check your work and make sure all calculations are correct.
You can check if your solution for a and b in a Fourier Transform is correct by taking the inverse Fourier Transform of your calculated values and comparing it to the original signal. If they match, then your solution is likely correct.
Some tips for solving for a and b in a Fourier Transform more efficiently include using properties of trigonometric functions to simplify the integrals, breaking the signal into smaller segments, and using software or calculators to evaluate the integrals. It is also helpful to practice and become familiar with the process.