Fraction of occupied states (Fermi-Dirac distribution + DOS)

[su3liminal1]

Homework Statement

Find the percentage of these states that have electrons in them, assuming the number of electrons above Ec+2kT is negligible.

Relevant Equations

-

I just want to clear some confusion I am having with the Fermi-Dirac distribution & density of states (DOS) of a semiconductor, which are given by

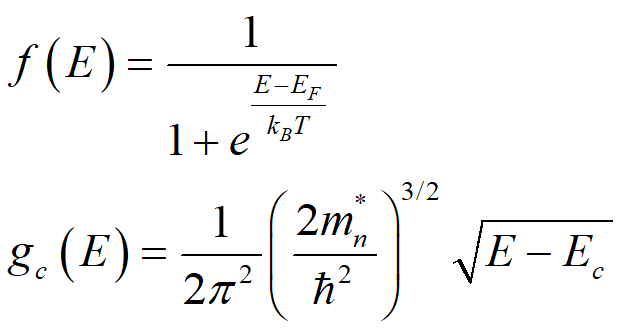
Say we have a piece of Silicon in equilibrium and its Fermi level lies 0.25 eV below the conduction band edge, i.e. E_c - E_F = 0.25 eV. Let us say we want to compute two things:
(1) Total number of states in the range E_c ≤ E ≤ E+ 2k_BT.
(2) The percentage of these states that have electrons in them, assuming the number of electrons above E_c+2k_BT is negligible.

For (1), it is straight forward: we just integrate the density of states function in the conduction band, g_c(E) over the indicated range:

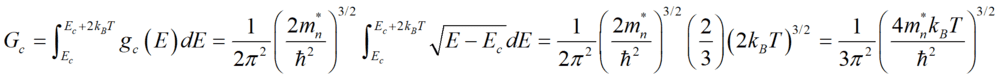
At room temperature and using an effective mass of silicon is, say, m_n^*=1.09m₀. This yields

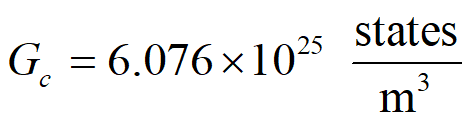
For (2), I know that the Fermi-Dirac distribution in this context represents the the probability of an electron occupying a state at energy E, which can also be interpreted as the ratio of filled state to total states at the energy. But I am really not sure what do here. Do I compute the difference of Fermi-Dirac distributions in that range, or do I integrate, or both are wrong?

 

[TSny]

Welcome to PF.

From part (1) you know the number of states (per m³) in the energy range $E_c$ to $E_c + 2k_BT$. I think you can answer part (2) if you know how many electrons (per m³) have energies in this range.

Suppose you consider a small range of energies $E$ to $E+dE$. Can you see how to get the number of electrons per m³ that have energies in this range? This will involve both $g_c(E)$ and $f(E)$.