joes1987
- 1
- 0
Hello all!
First post! I've been meaning to join this board for a while. I'm an electronic engineer with interests in physics.
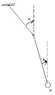
I set myself the challenge of trying to obtain the dynamics equations for a double pendulum setup without using Lagrange. (configuration in attached picture)
The issue I seem to be having centres around the point at which the 2 rods are connected. I don't have a mass at this point. Does this mean I cannot use a normal Free Body Diagram? If I am allowed to, then I have only 2 forces at this pivot point (I think!) - the tensions of each rod. However, I was looking at this link: http://www.phys.lsu.edu/faculty/gonzalez/Teaching/Phys7221/DoublePendulum.pdf
which does a pretty similar problem using Newtons laws, the only difference is that they have a mass between the two rods. However, when I look at their equations (32) and (33) which are Newton's laws on the free-body diagram of this junction, and reduce the mass (m1) to zero, I don't get the same equation as I have.
When I work it out independently, I get: T1 = T2*cos(a - b), whereas the equations from that paper just don't make any sense when I set m1 = 0.
Am I doing something silly?
Thanks!
First post! I've been meaning to join this board for a while. I'm an electronic engineer with interests in physics.
I set myself the challenge of trying to obtain the dynamics equations for a double pendulum setup without using Lagrange. (configuration in attached picture)
The issue I seem to be having centres around the point at which the 2 rods are connected. I don't have a mass at this point. Does this mean I cannot use a normal Free Body Diagram? If I am allowed to, then I have only 2 forces at this pivot point (I think!) - the tensions of each rod. However, I was looking at this link: http://www.phys.lsu.edu/faculty/gonzalez/Teaching/Phys7221/DoublePendulum.pdf
which does a pretty similar problem using Newtons laws, the only difference is that they have a mass between the two rods. However, when I look at their equations (32) and (33) which are Newton's laws on the free-body diagram of this junction, and reduce the mass (m1) to zero, I don't get the same equation as I have.
When I work it out independently, I get: T1 = T2*cos(a - b), whereas the equations from that paper just don't make any sense when I set m1 = 0.
Am I doing something silly?
Thanks!