Frictional Forces Physics 1 Problem

[Almost935]

Homework Statement

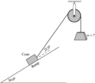
7.) A 1520-N crate is to be held in place on a ramp that rises at 30.0° above the horizontal (see figure). The massless rope attached to the crate makes a 22.0° angle above the surface of the ramp. The coefficients of friction between the crate and the surface of the ramp are µ_k = 0.450 and μ_s = 0.650. The pulley has no appreciable mass or friction. What is the MAXIMUM weight w that can be used to hold this crate stationary on the ramp?

Picture of problem:

Homework Equations

F_s = μ_sF_n

F = ma

The Attempt at a Solution

I attempted by first mapping out the forces for F_x and F_y. I then solved for the normal force in order to replace it in the static friction force equation so as to be able to solve for the tension in the rope which I then found to be 1380 N. I am unsure whether this is the answer. Logically it somewhat makes sense that the tension in the rope must be equal to the weight of the mass on the other end to be completely still. Looking for some analysis of my answer and some pointers in the correct direction

 

[Simon Bridge]

I attempted by first mapping out the forces for F_x and F_y.

Guessing that you placed the axes to that +x direction points "up along the ramp"?

I then solved for the normal force in order to replace it in the static friction force equation so as to be able to solve for the tension in the rope which I then found to be 1380 N. I am unsure whether this is the answer. Logically it somewhat makes sense that the tension in the rope must be equal to the weight of the mass on the other end to be completely still.

Best practice is to do all the algebra before you put numbers in - it can avoid the sort of confusion you ended up in.

Looking for some analysis of my answer and some pointers in the correct direction

You need two free-body diagrams to be sure to get this answer correct, one for the mass on the slope - which you have basically done, and the other for the hanging mass.

This gives you two equations - which is good, because you have two unknowns: the tension in the rope and the weight that hangs off the pulley.

So repeat the process for the hanging mass and see if you are right.

 

[Almost935]

So you are saying that the Tension is equal throughout despite the angle on the first mass?

 

[Simon Bridge]

The tension points along the rope doesn't it? Why would the rope care about what angle stuff is attached to it?