Full Bridge Inverter: Got the answer by 1 method, but not by another

[jaus tail]

Homework Statement

Homework Equations

Fourier and then V(output) = 4Vs/(n*3.14) * sin (nwt) where Vs is battery here it's 400V
Current = V(output) / X(L). Here X is 2*3.14*100*0.2

The Attempt at a Solution

I got V(output) = 4*400/3.14 = 509.55V This is fundamental Peak output voltage.
So Current peak = 509.55 / impedance. Impedance = 2*3.14*100*0.2 = 125.6 Ohm
So Current peak = 509.55 / 125.6 = 4.06A
But this is not in option.

If i use other method of V = L di/dt

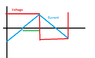
Here for time interval by green line
400 = 0.2 * di/dt
dt = time interval in green part = time period / 4. Frequency = 100 Hz. So Time period = 0.01 seconds
So dt = T/4 = 2.5 milli seconds
So 400 = 0.2 * di / dt
This gives di = 5 A.

But why don't i get correct answer if I go by above method of fourier?

 

[NascentOxygen]

With all ideal components, I think you're correct in saying the current waveform will be triangular. So your analysis using L.di/dt should be right.

In your analysis using Fourier's fundamental component, you are approximating that trianglar wave to a sinusoid, so you can't expect the peak values to be the same. The formula is one you copied from someone else's analysis, is it? There is, of course, a fixed relation between the peak value of a symmetrical triangular wave and the peak value of its first harmonic (the fundamental). So maybe you could work backwards: knowing the peak value of its fundamental component, what would be the peak value of the Fourier-related triangular wave?

 

[jaus tail]

The formula for Fourier I used of Resistive load. Yeah you're right it would be different.
From google i got
I(sinusoidal) = 8/(3.14)² I(triangular)
So I got I(sinusoidal) = 4.06 times I (triangular)
So I (triangular) = 4.06 * 3.14 * 3.14 / 8 = 5.009 A

 

[NascentOxygen]

What do the diodes do here?

 

[jaus tail]

Diodes help maintain current smooth across inductor. If diodes are removed they'll be high reverse potential across switches which may cause boom.
In figure below, left diagram is when switches are conducting and right diagram is when diodes are conducting. Current through inductor is left to right.
After time T3, the current through inductor reverses.

 

[NascentOxygen]

If you were using unidirectional switches¹ for T_1...4 then you would need the diodes to be conducting for the full ¼ cycle as you describe. They could be described as "freewheeling diodes".

But if you were able to build the circuit using 4 bidirectional switches² or ideal switches then you could operate each pair of switches for a full ½ cycle at a time, meaning T_1,3 or T_2,4 would be carrying current practically all the time, and subjecting the diodes to only brief spikes of current during switch changeover, then you could call them protection diodes.

¹ such as ordinary transistors
² such as FETs