Physiona
- 131
- 9
Shown below is the graph of
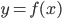
The graph interests the
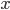 axis at 3 points, B, C and D.
axis at 3 points, B, C and D.
Given the points of intersection, and the brackets below, form and expand an equation for
the graph of
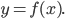
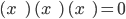
ATTEMPT:
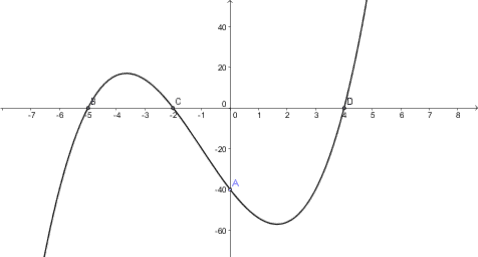
I've assumed to involve the points of intersection for the x-axis which is 4, -2, and -5. It looks to be a cubic graph where x3. I'm not entirely convinced on how I progress from here if this way is correct. Any guidance? Thank you.
The graph interests the
Given the points of intersection, and the brackets below, form and expand an equation for
the graph of
ATTEMPT:
I've assumed to involve the points of intersection for the x-axis which is 4, -2, and -5. It looks to be a cubic graph where x3. I'm not entirely convinced on how I progress from here if this way is correct. Any guidance? Thank you.
Attachments
-
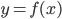 chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=y%3Df%28x%29.png430 bytes · Views: 872
chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=y%3Df%28x%29.png430 bytes · Views: 872 -
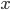 chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=x.png202 bytes · Views: 863
chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=x.png202 bytes · Views: 863 -
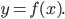 chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=y%3Df%28x%29.png440 bytes · Views: 836
chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=y%3Df%28x%29.png440 bytes · Views: 836 -
 image?rev=4&h=257&w=478&ac=1.png3.7 KB · Views: 969
image?rev=4&h=257&w=478&ac=1.png3.7 KB · Views: 969 -
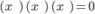 000000&chl=%28x%5C+%5C+%5C+%5C+%5C+%29%5C+%28x%5C+%5C+%5C+%5C+%29%5C+%28x%5C+%5C+%5C+%5C+%29%3D0.png592 bytes · Views: 891
000000&chl=%28x%5C+%5C+%5C+%5C+%5C+%29%5C+%28x%5C+%5C+%5C+%5C+%29%5C+%28x%5C+%5C+%5C+%5C+%29%3D0.png592 bytes · Views: 891