Discussion Overview
The discussion revolves around the application of Gauss' law to a non-uniformly charged spherical shell and the implications for the electric field in various scenarios. Participants explore the relationship between charge distribution, electric field, and the mathematical formulations of Gauss' law, including both integral and differential forms.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
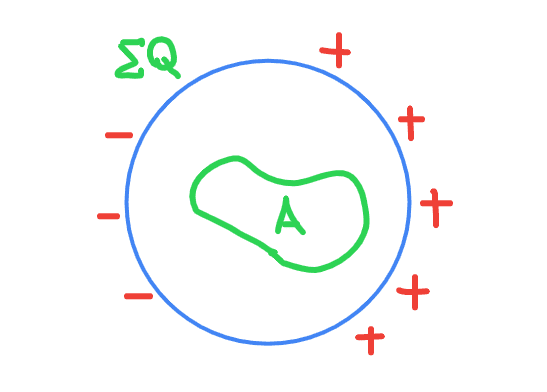
- One participant questions whether the electric field is zero on a Gaussian surface surrounding a non-conducting spherical shell with no charge inside, reflecting on the application of Gauss' law.
- Another participant clarifies that Gauss' law indicates the integral of the electric field over the surface is zero, not necessarily the field itself.
- A comparison is made to a parallel plate capacitor, suggesting that the electric field is not zero even if the total flux through a Gaussian surface is zero.
- Participants discuss the concept of electric field lines and their behavior in relation to surfaces enclosing net charge versus those that do not.
- There is a discussion about the divergence of the electric field, with one participant proposing that it is zero when there is no charge inside, while another refines this by explaining the distinction between pointwise divergence and integral forms of Gauss' law.
- One participant asserts that Gauss' law applies regardless of charge distribution, emphasizing that the total charge inside a closed surface can be zero while still containing both positive and negative charges.
- Another participant notes the relationship between the integral and differential forms of Gauss' law, referencing Gauss's Integral Theorem.
Areas of Agreement / Disagreement
Participants express differing views on the implications of Gauss' law in the context of non-uniform charge distributions. While some agree on the mathematical principles, there is no consensus on the interpretation of the electric field behavior in specific scenarios.
Contextual Notes
Participants highlight limitations in understanding the divergence of the electric field and its relationship to charge distribution, indicating that the discussion is nuanced and dependent on specific conditions and definitions.