- #1
Dr_Pill
- 41
- 0
Hi,
I don't understand this:
You got a dipole, and a resulting electric field from it like this(hyperphysics):
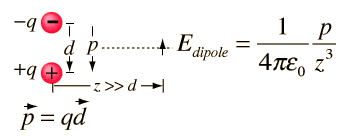
As z approaches infinity, the field becomes zero.
But if you draw a gaussian surface round the charges, then the net enclosed charge is zero.So the electric field must be zero, no matter how I draw the surface.
So If i just draw a surface tiny enough to enclose both charges, my z is totally not going to infinity and the field is zero according to Gauss' LAw.
How is this compatible with each other?What is the pitfall in my thinking.
Thanks in advance.
I don't understand this:
You got a dipole, and a resulting electric field from it like this(hyperphysics):
As z approaches infinity, the field becomes zero.
But if you draw a gaussian surface round the charges, then the net enclosed charge is zero.So the electric field must be zero, no matter how I draw the surface.
So If i just draw a surface tiny enough to enclose both charges, my z is totally not going to infinity and the field is zero according to Gauss' LAw.
How is this compatible with each other?What is the pitfall in my thinking.
Thanks in advance.