- #1
lowea001
- 29
- 3
EDIT: I realize now that I have fundamentally misunderstood a crucial aspect of deriving the Bell inequality for this case which is the existence of the third axis. The setup of the problem did state that the axes were chosen at random. Therefore I can't just look at the possibility of choosing one specific axis. I no longer require assistance with the question but will leave it here:
I have been introduced to bell inequalities through an introductory course on quantum information. The specific setup presented was the following: Alice and Bob are given the entangled Bell state ##|\Psi\rangle = \frac{1}{\sqrt{2}}\left(|01\rangle - |10\rangle\right)## such that the results of their measurements always disagree when they pick the same measurement axis, but differ with some probability ##P## when they pick different axes.
A local hidden variable theory predicts that whatever this probability is, assuming that different measurement axes are picked, ##P_{\text{classical}} \geq \frac{1}{3}## (if this needs further clarification I can elaborate in the thread but this is the version of Bell's inequality which we were given). It is then shown that if Alice measures ##+\frac{\hbar}{2}## along the z-axis, then if Bob pick the measurement axis ##\hat{S}_2 = \frac{\hbar}{2}\left(\text{cos}\frac{2\pi}{3}\sigma_3 + \text{sin}\frac{2\pi}{3}\sigma_1\right)## , then he observes the spin down state with probability ##P = \frac{1}{4}## which is less than the ##\frac{1}{3}## we'd expect classically. My question is, can we generalize this to arbitrary measurement axes based on the azimuthal angle ##\theta## ? I learned earlier in the course that in some random direction ##\hat{S }_n## the probability of measuring ##+\frac{\hbar}{2}## is $$P = \text{cos}^2(\theta/2)$$. In that case, is the following graph valid?
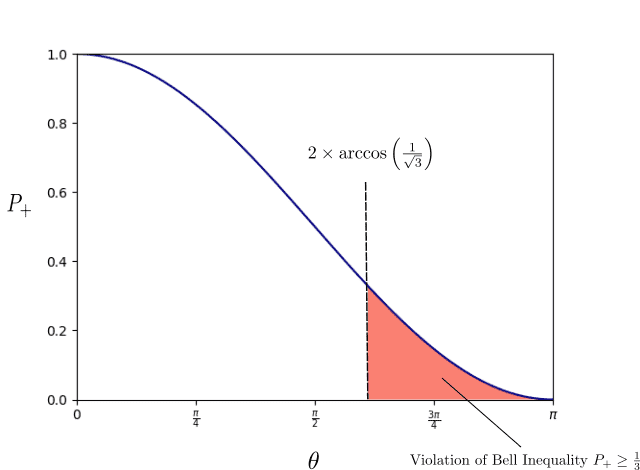Something doesn't seem right to me since as you approach ##\theta = \pi## Bell's inequality is violated with a greater magnitude and this can get arbitrarily close to ##\pi##, but I'm pretty sure there should be an angle at which the violation is maximal. I know right at ##\pi## this is no longer a valid axis since the measurement axes should form a basis in 3D. Is my plot of probabilities for different angles incorrect, or am I wrong in my assumption that there should be an angle for which the violation is maximal?
I have been introduced to bell inequalities through an introductory course on quantum information. The specific setup presented was the following: Alice and Bob are given the entangled Bell state ##|\Psi\rangle = \frac{1}{\sqrt{2}}\left(|01\rangle - |10\rangle\right)## such that the results of their measurements always disagree when they pick the same measurement axis, but differ with some probability ##P## when they pick different axes.
A local hidden variable theory predicts that whatever this probability is, assuming that different measurement axes are picked, ##P_{\text{classical}} \geq \frac{1}{3}## (if this needs further clarification I can elaborate in the thread but this is the version of Bell's inequality which we were given). It is then shown that if Alice measures ##+\frac{\hbar}{2}## along the z-axis, then if Bob pick the measurement axis ##\hat{S}_2 = \frac{\hbar}{2}\left(\text{cos}\frac{2\pi}{3}\sigma_3 + \text{sin}\frac{2\pi}{3}\sigma_1\right)## , then he observes the spin down state with probability ##P = \frac{1}{4}## which is less than the ##\frac{1}{3}## we'd expect classically. My question is, can we generalize this to arbitrary measurement axes based on the azimuthal angle ##\theta## ? I learned earlier in the course that in some random direction ##\hat{S }_n## the probability of measuring ##+\frac{\hbar}{2}## is $$P = \text{cos}^2(\theta/2)$$. In that case, is the following graph valid?
Attachments
Last edited:
