You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Bell inequalities Definition and 23 Threads
Bell's theorem proves that quantum physics is incompatible with local hidden-variable theories. It was introduced by physicist John Stewart Bell in a 1964 paper titled "On the Einstein Podolsky Rosen Paradox", referring to a 1935 thought experiment that Albert Einstein, Boris Podolsky and Nathan Rosen used to argue that quantum physics is an "incomplete" theory. By 1935, it was already recognized that the predictions of quantum physics are probabilistic. Einstein, Podolsky and Rosen presented a scenario that, in their view, indicated that quantum particles, like electrons and photons, must carry physical properties or attributes not included in quantum theory, and the uncertainties in quantum theory's predictions were due to ignorance of these properties, later termed "hidden variables". Their scenario involves a pair of widely separated physical objects, prepared in such a way that the quantum state of the pair is entangled.
Bell carried the analysis of quantum entanglement much further. He deduced that if measurements are performed independently on the two separated halves of a pair, then the assumption that the outcomes depend upon hidden variables within each half implies a constraint on how the outcomes on the two halves are correlated. This constraint would later be named the Bell inequality. Bell then showed that quantum physics predicts correlations that violate this inequality. Consequently, the only way that hidden variables could explain the predictions of quantum physics is if they are "nonlocal", somehow associated with both halves of the pair and able to carry influences instantly between them no matter how widely the two halves are separated. As Bell wrote later, "If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."Multiple variations on Bell's theorem were proved in the following years, introducing other closely related conditions generally known as Bell (or "Bell-type") inequalities. These have been tested experimentally in physics laboratories many times since 1972. Often, these experiments have had the goal of ameliorating problems of experimental design or set-up that could in principle affect the validity of the findings of earlier Bell tests. This is known as "closing loopholes in Bell test experiments". To date, Bell tests have found that the hypothesis of local hidden variables is inconsistent with the way that physical systems do, in fact, behave.The exact nature of the assumptions required to prove a Bell-type constraint on correlations has been debated by physicists and by philosophers. While the significance of Bell's theorem is not in doubt, its full implications for the interpretation of quantum mechanics remain unresolved.
View More On Wikipedia.org
Bell carried the analysis of quantum entanglement much further. He deduced that if measurements are performed independently on the two separated halves of a pair, then the assumption that the outcomes depend upon hidden variables within each half implies a constraint on how the outcomes on the two halves are correlated. This constraint would later be named the Bell inequality. Bell then showed that quantum physics predicts correlations that violate this inequality. Consequently, the only way that hidden variables could explain the predictions of quantum physics is if they are "nonlocal", somehow associated with both halves of the pair and able to carry influences instantly between them no matter how widely the two halves are separated. As Bell wrote later, "If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."Multiple variations on Bell's theorem were proved in the following years, introducing other closely related conditions generally known as Bell (or "Bell-type") inequalities. These have been tested experimentally in physics laboratories many times since 1972. Often, these experiments have had the goal of ameliorating problems of experimental design or set-up that could in principle affect the validity of the findings of earlier Bell tests. This is known as "closing loopholes in Bell test experiments". To date, Bell tests have found that the hypothesis of local hidden variables is inconsistent with the way that physical systems do, in fact, behave.The exact nature of the assumptions required to prove a Bell-type constraint on correlations has been debated by physicists and by philosophers. While the significance of Bell's theorem is not in doubt, its full implications for the interpretation of quantum mechanics remain unresolved.
View More On Wikipedia.org
-

B Why do photon polarization experiments show similar outcomes in different situations?
I'm trying to make sens of the dirac's three polarizer experiment (Moderator's note: link removed) and the epr experiment and bell's inequalities, and i have a loooots of questions, but here i will focus on one first. (I have read some of the long and very interesting threads on the subject that...- gohu
- Thread
- Replies: 11
- Forum: Quantum Physics
-
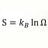
B Quantum Nonlocality or Non Counterfactual Definiteness?
It seems the major premise for the derivation of Bell Inequalities is Counterfactual Definiteness for both electrons and photons : For electrons the spins at x, y, z directions are expected from conservation laws. See table. And for photons the eight polarization types along three orientations...- morrobay
- Thread
- Replies: 3
- Forum: Quantum Physics
-
A
I Measuring electron spin and measuring entangled electron spin
Hi people, Lets assume, we have a stern gerlach setup and we are going to measure an atom's last orbit electron's spin with 60 degree from vertical axis. Therefore, in this case, our outcomes would be 3/4 for spin up, 1/4 for spin down. Let's assume, we have the same setup but we are going to...- Athraxin
- Thread
- Replies: 12
- Forum: Quantum Physics
-
I What Is Bell's Theorem and Why Does It Matter?
Hi everyone, I need some help getting the gist of Bell’s theorem and his notion of inequalities. How would you explain it to someone with limited knowledge of mathematics? What are the potential implications?- golya
- Thread
- Replies: 3
- Forum: Quantum Physics
-
M
I Do Bell Experiments Show Local Overlap of Wave Functions Before Measurement?
Consider experiments that demonstrate violations of Bell inequalities. I'm wondering about the spatial extent of the wave function of the particles BEFORE measurement. I assume the spatial extent is "very large," and my main question is whether they overlap. If the wave functions do overlap...- msumm21
- Thread
- Replies: 72
- Forum: Quantum Physics
-

A Bell inequalities demonstration
Hello, In this thesis https://tel.archives-ouvertes.fr/tel-01743877/document at "1.2.2 Bell inequalities" page 7-8 it's define a correlation function : C(x y) = P(+ + |x y) + P(− − |x y) − P(+ − |x y) − P(− + |x y), with −1 ≤ C(x y) ≤ 1. How do one get to this relationship −1 ≤ C(x y) ≤ 1 ...- microsansfil
- Thread
- Replies: 1
- Forum: Quantum Physics
-
M
I Model used to refute Bell's theorem
I’m looking over a recent paper mentioned in another thread. It claims to refute Bell’s theorem. At first glance, the model presented in the paper doesn’t appear consistent with QM. Here’s a simple example. Suppose we set both polarizers to the same angle ##\alpha = \pi /4##. In the model...- msumm21
- Thread
- Replies: 19
- Forum: Quantum Interpretations and Foundations
-

I An Alternative form of Bell's Inequality
Bell's inequality in it's original form is: |cor(a,b) - cor(a,c)| \le 1 - cor(b,c) where ##a,b## and ##c## are random variables with values ##\pm 1##, and the correlation is then simply the expectation value of their products, ##cor(a,b)=E[ab]## or as usually expressed ##\langle ab\rangle##...- jambaugh
- Thread
- Replies: 5
- Forum: Quantum Physics
-
J
B Thought Experiment: Exploring Violations of Bell Inequalities
I have been thinking about the Violation of bell inequalities , trying to justify how non locality can be determined from violation of bell tests. I have been through Dr. Chinese page which has partially convinced me that there can be no hidden variables , but I need to understand what...- Johan0001
- Thread
- Replies: 25
- Forum: Quantum Physics
-
L
I Generalizing the Bell Inequality for Arbitrary Measurement Axes
EDIT: I realize now that I have fundamentally misunderstood a crucial aspect of deriving the Bell inequality for this case which is the existence of the third axis. The setup of the problem did state that the axes were chosen at random. Therefore I can't just look at the possibility of choosing...- lowea001
- Thread
- Replies: 1
- Forum: Quantum Physics
-
I Do these Bell inequalities rely on probability concept?
This question came up in another thread. I will post again the link to Nick Herbert's proof here: https://www.physicsforums.com/threads/a-simple-proof-of-bells-theorem.417173/#post-2817138 I don't see where the probability shows up in Nick Herbert's proof. For discussion of Eberhard's proof I...- zonde
- Thread
- Replies: 13
- Forum: Quantum Physics
-
H
I Difference between CHSH and Bell inequalities
Bell's Inequality, P(a,b)-P(a,d)+P(c,b)+P(c,d) is calculated as: S = a*b - a*d + c*b + c*d <= 2. It is valid for all values of a, b, c and d between -1 and +1 It is also valid for counts, a=a's counts/total counts of a,b,c &d. b, c,and d are derived similarly. Negative counts are not allowed...- harpo
- Thread
- Replies: 5
- Forum: Quantum Physics
-
J
A Quantum measurement with incomplete basis?
In page 9 of http://www.theory.caltech.edu/people/preskill/ph229/notes/chap4.pdf we can find simple form of Bell inequalities for three binary variables: $$ P(A=B) + P(A=C) + P(B=C) \geq 1 $$ which is kind of obvious: "This is satisfied by any probability distribution for the three coins because...- jarekduda
- Thread
- Replies: 2
- Forum: Quantum Physics
-
N
I What is the physical significance of Bell's math?
Bell (1964) http://cds.cern.ch/record/111654/files/vol1p195-200_001.pdf has 3 unnumbered equations following his equation (14). Let them be (14a)-(14c). Bell then uses his equation (1) to move from (14a)-(14b). It seems to me that he uses this: [A(b,λ)]2 = 1. (X)...- N88
- Thread
- Replies: 199
- Forum: Quantum Physics
-
G
I Assuming nonlocal realism: What message would signal convey?
Hi. I have a strange relation to Bell's inequalities, I understand (so I hope) all the maths but have lots of trouble with the implications of their violation. Currently: Say we assume QM to be realistic, it can't be local. There needs to be some sort of instantaneous signalling. Realism means...- greypilgrim
- Thread
- Replies: 30
- Forum: Quantum Physics
-
M
B Why the "rush" to quantum spookiness
Hi, those who have responded to any of my previous posts may remember me as one with little mathematical background beyond college calculus, and only a layman's understanding of physics, though I have read a *lot* of layman-oriented material. But I do have a very strong sense that the universe -...- Micheth
- Thread
-
- Tags
- Bell inequalities Quantum
- Replies: 25
- Forum: Quantum Physics
-

Understanding Bell's inequality
I am not sure if I am allowed to ask this, but here's my shot: I find all the explanations of Bell's theorem summed up here, very different in interpretation and also (for me) incomprehensible. I have these simple questions: How does the Bell inequality, stated as N(A, not B) + N(B, not C) ≥...- entropy1
- Thread
- Replies: 29
- Forum: Quantum Physics
-
J
Violation of Bell inequalities for classical fields?
There is a recent article (Optics July 2015) claiming violation of Bell inequalities for classical fields: "Shifting the quantum-classical boundary: theory and experiment for statistically classical optical fields" https://www.osapublishing.org/optica/abstract.cfm?URI=optica-2-7-611...- jarekduda
- Thread
- Replies: 70
- Forum: Quantum Physics
-
G
Bell's Theorem Explained in nLab: Probability Density
I'm trying to follow this mathematical explanation of Bell's theorem. The problem I find is with the assumption of a probability density for the hidden variable. That implies - and my question is: am I wrong? why? - that you can expect the same distribution of such a variable for any repetition...- giulio_hep
- Thread
- Replies: 7
- Forum: Set Theory, Logic, Probability, Statistics
-
Z
Problem of superluminal communication in Non-local HVTs
Hi there. I have been studying on Bell Inequalities and hidden variables problem for quite some time now however my general knowledge on the problem of superluminal communication is superficial at best. I know that non of the standing interpretations (Everett, Copenhagen, Bohmian, QBist etc.)...- Zcs
- Thread
- Replies: 8
- Forum: Quantum Physics
-

Can we violate Bell inequalities by giving up CFD?
I quoted these post from other thread. I don't want to distract discussion in other thread so I'm starting a new one about statements in these posts. Basically the question is if we can violate Bell inequalities by two separated but correlated systems that can be as non-classical as we like (as...- zonde
- Thread
- Replies: 151
- Forum: Quantum Physics
-
P
Binney's interpretation of Violation of Bell Inequalities
Although he is primarily an astrophysicist, Dirac medal-winning Oxford Professor James Binney has taught a Quantum Physics course to second-year students at the university for years. A series of 27 of his lectures for the course is featured on the university's official website. Binney's take on...- Pat71
- Thread
- Replies: 153
- Forum: Quantum Interpretations and Foundations
-
L
What chronology of Bell inequalities testing ?
Hi all ! What chronology of Bell inequalities testing ( their violation ) ? What positive and negative aspects of each experiment ? What experiments have been spent latest years ? Some material: http://arxiv.org/PS_cache/quant-ph/pdf/0310/0310192v1.pdf Thanks.- limarodessa
- Thread
- Replies: 2
- Forum: Quantum Physics