Geodesic Eq: Deriving 2nd Term on RHS

[peterpang1994]

As the geodesic equation in a form of

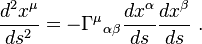
is quite familiar for me. But I still cannot derive it in terms of time coordinate parameter;

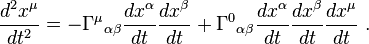
I can't get the second term on the right hand side
what I can get is
½{d[lng_αβ(dx^α/dt)(dx^β/dt)]/dt}dx^μ/dt

How can I obtain that term?

 

[Orodruin]

I suggest you do not work in terms of the metric. The equation follows directly from the variable substitution to parameterise the curve with $t$ instead of $s$ and looking at how the geodesic equation transforms under this change. Keep in mind that
$$
\frac{d^2 t}{ds^2} = - \Gamma^0_{\alpha\beta} \dot x^\alpha \dot x^\beta .
$$