Plat00n
- 11
- 0
GEOMETRICAL STUDY OF SCHROEDINGER'S FORMULA
If we take a look on previous expression, we could continue with the importance of complex numbers.
The complex numbers are very important to represent points or vectors in plane, and can be expressed this way:
a = b·x+c·y
If we choose the real axis numbers like X, and imaginaries like Y:
a = b + c·i
But we could have been done this:
a = b·i + c
If we take Geometric Algebras (GA), more exactly the even sub group of GA, we can represent vectors like part quaternions, and rotations through quaternion operators.
If we take an element of volume (area in draw):
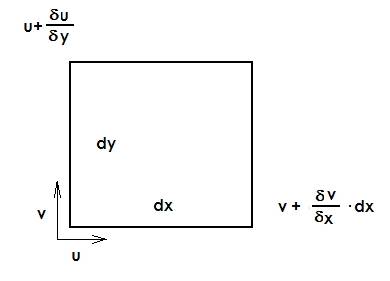
And take a volume in a posterior time:
V_t+dt = \left( dx + \frac {\partial u}{\partial x} dx \cdot dt \right) \left( dy + \frac {\partial v}{\partial y} dy \cdot dt \right)
And the relative change of volume is:
\frac {d \left( \frac {V_t_+_d_t - V_t} {V_t} \right) } {dt} = \frac {dV_R}{dt} = \frac {\partial u}{\partial x} + \frac {\partial v}{\partial y}
We have that:
\frac {\partial V_R}{\partial t} = \frac {\partial u}{\partial x} + \frac {\partial v}{\partial y} + \frac {\partial w}{\partial z} = \nabla \cdot \vec {v}
The dilatation of volume can be directly expressed with velocity gradient in space:
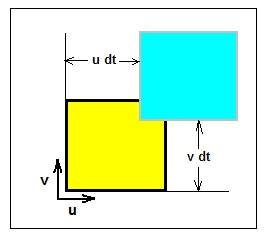
A volume element can be:
TRANSLATED:
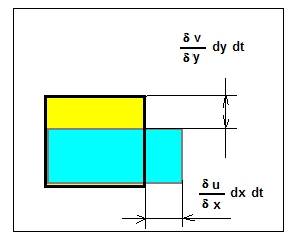
DEFORMATED:
ROTATED
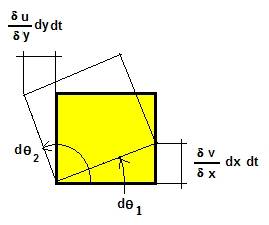
or HAVE CUTTING EFFORTS
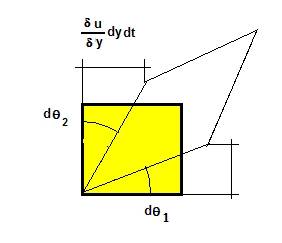
If we analyze the angles \theta_1 y \theta_2, it can easily verify geometrically that:
TAN~~ d \theta_1 \simeq d \theta_1 \simeq \frac {\left( \frac {\partial v} {\partial x} dx \cdot dt \right) }{dx}
And:
TAN~~ d \theta_2 \simeq d \theta_2 \simeq \frac {\left( \frac {- \partial u} {\partial y} dy \cdot dt \right) }{dy}
And we have:
\dot {\theta_1} = \frac {d \theta_1}{dt} = \frac {\partial v}{\partial x}
and
\dot {\theta_2} = \frac {d \theta_2}{dt} = - \frac {\partial u}{\partial y}
And angular velocity in Z axis will be:
\omega_z = \frac {1}{2} \left( \frac {\partial v}{\partial x} - \frac {\partial u}{\partial y} \right) = \frac {1}{2} \dot {\theta_1} + \dot {\theta_2}
Now, if we take this fraction of the Schrödinger's:
\nabla \left[ \frac {i \hbar} {2m} \left( \psi \nabla \psi^*} - \psi^* \nabla \psi \right) \right]
Or much clear:
\nabla \left[ \frac {1} {2} \left( \psi \vec v \psi^*} - \psi^* \vec v \psi \right) \right]
Does anybody likes to play in discovering what it means?
-----------
References:
- Quaternion and Rotation Sequences, Jack B. Kuipers
- Vectors, tensors and the Basic Equations of Fluid Mechanics, Rutherford Aris.
- Vibraciones y ondas. A. P. French.
- Lectures On Clifford (Geometric) Algebras. Rafal Ablamowicz et. al.
- Mecánica de Fluidos. Victor L. Streeter et. al.
- De Natura Visibilium et Invisibilium. R. Aparicio. Ed. Elaleph.
- Siglo XXI: La Física que nos espera. R. Aparicio. Ed. Elaleph.[/quote]
\vec J = \mathfrak{Re}[\Psi^* (\vec r) (\frac{-i \hbar}{m} \vec \nabla) \Psi (\vec r) ]
If we take a look on previous expression, we could continue with the importance of complex numbers.
The complex numbers are very important to represent points or vectors in plane, and can be expressed this way:
a = b·x+c·y
If we choose the real axis numbers like X, and imaginaries like Y:
a = b + c·i
But we could have been done this:
a = b·i + c
If we take Geometric Algebras (GA), more exactly the even sub group of GA, we can represent vectors like part quaternions, and rotations through quaternion operators.
If we take an element of volume (area in draw):
And take a volume in a posterior time:
V_t+dt = \left( dx + \frac {\partial u}{\partial x} dx \cdot dt \right) \left( dy + \frac {\partial v}{\partial y} dy \cdot dt \right)
And the relative change of volume is:
\frac {d \left( \frac {V_t_+_d_t - V_t} {V_t} \right) } {dt} = \frac {dV_R}{dt} = \frac {\partial u}{\partial x} + \frac {\partial v}{\partial y}
We have that:
\frac {\partial V_R}{\partial t} = \frac {\partial u}{\partial x} + \frac {\partial v}{\partial y} + \frac {\partial w}{\partial z} = \nabla \cdot \vec {v}
The dilatation of volume can be directly expressed with velocity gradient in space:
A volume element can be:
TRANSLATED:
DEFORMATED:
ROTATED
or HAVE CUTTING EFFORTS
If we analyze the angles \theta_1 y \theta_2, it can easily verify geometrically that:
TAN~~ d \theta_1 \simeq d \theta_1 \simeq \frac {\left( \frac {\partial v} {\partial x} dx \cdot dt \right) }{dx}
And:
TAN~~ d \theta_2 \simeq d \theta_2 \simeq \frac {\left( \frac {- \partial u} {\partial y} dy \cdot dt \right) }{dy}
And we have:
\dot {\theta_1} = \frac {d \theta_1}{dt} = \frac {\partial v}{\partial x}
and
\dot {\theta_2} = \frac {d \theta_2}{dt} = - \frac {\partial u}{\partial y}
And angular velocity in Z axis will be:
\omega_z = \frac {1}{2} \left( \frac {\partial v}{\partial x} - \frac {\partial u}{\partial y} \right) = \frac {1}{2} \dot {\theta_1} + \dot {\theta_2}
Now, if we take this fraction of the Schrödinger's:
\nabla \left[ \frac {i \hbar} {2m} \left( \psi \nabla \psi^*} - \psi^* \nabla \psi \right) \right]
Or much clear:
\nabla \left[ \frac {1} {2} \left( \psi \vec v \psi^*} - \psi^* \vec v \psi \right) \right]
Does anybody likes to play in discovering what it means?
-----------
References:
- Quaternion and Rotation Sequences, Jack B. Kuipers
- Vectors, tensors and the Basic Equations of Fluid Mechanics, Rutherford Aris.
- Vibraciones y ondas. A. P. French.
- Lectures On Clifford (Geometric) Algebras. Rafal Ablamowicz et. al.
- Mecánica de Fluidos. Victor L. Streeter et. al.
- De Natura Visibilium et Invisibilium. R. Aparicio. Ed. Elaleph.
- Siglo XXI: La Física que nos espera. R. Aparicio. Ed. Elaleph.[/quote]
Last edited: