- #1
kent davidge
- 933
- 56
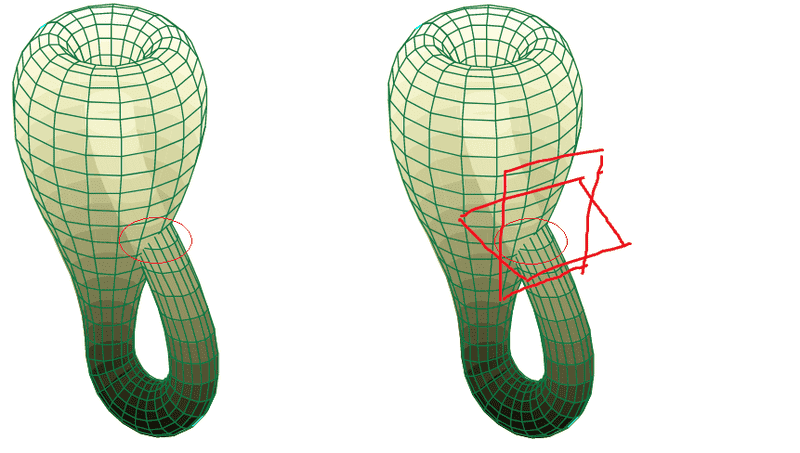
I know that there exists non-geometrical proofs that the usual mapping of the Klein Bottle in ##\mathbb{R}^3## is an immersion. But I would like to see an actual geometrical 'test'. I was thinking if saying that on the self intersection, which I circled in red below, the map being injective can be justified by saying that it's because there are two distinct tangent spaces, which is drawn in the right picture?