anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
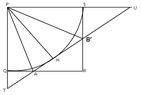
Suppose that $PQRS$ is a square with side $p$. Let $A$ and $B$ be points on side $QR$ and $RS$ respectively, such that $\angle APB=45^{\circ}$. Let $T$ and $U$ be the intersections of $AB$ with $PQ$ and $PS$ respectively. Prove that $PT+PU\ge 2\sqrt{2}p$.