Inspector Gadget
- 31
- 0
I'm working on this problem.
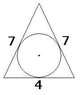
The only given information is the circle is inscribed into the triangle. And you have to find the radius of the circle.
The answer is...
\frac{2\sqrt{5}}{3}
Can someone come up with an explanation as to why? It's been a few years since I had geometry, and have tried everything I remembered with bisectors and whatnot.
The only given information is the circle is inscribed into the triangle. And you have to find the radius of the circle.
The answer is...
\frac{2\sqrt{5}}{3}
Can someone come up with an explanation as to why? It's been a few years since I had geometry, and have tried everything I remembered with bisectors and whatnot.