Getting Started: Overcoming the Blank Page

[hidemi]

Homework Statement

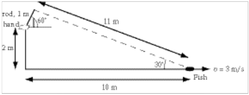
A 0.50 kg fish, hooked as shown below, starts to swim away at a speed of 3.0 m/s.

The angular momentum of the fish relative to the hand holding the fishing rod is

about:

(a) 3 kg m^2 / s

(b) 6 kg m^2 / s

(c) 17 kg m^2 / s

(d) 30 kg m^2 / s

(e) 60 kg m^2 / s

The answer is A.

Relevant Equations

L = I w

I have no idea how to start ;(

 

[BvU]

Hi,

I have no idea how to start ;(

Doesn't get you any help, as per PF guidelines ....
You might know that by now ... ?

What is w ? what is I ? How do they relate to your known variables ?
Any alternative to $\vec L = I \vec \omega$ ?

$\$

 

[hidemi]

Hi,

Doesn't get you any help, as per PF guidelines ....
You might know that by now ... ?

What is w ? what is I ? How do they relate to your known variables ?
Any alternative to $\vec L = I \vec \omega$ ?

$\$

Here's my calculation:
L = I*w = m*r^2*(v/r) = 0.5 * 11 * 3 = 16.5

Option (C) is close to my answer, but (A) is the official answer. Can anyone help, please? Thanks!

 

[kuruman]

I echo @BvU's suggestion to use an alternative to $\vec L=I\vec \omega$. However, if you insist on using $\vec L=mr^2 \vec \omega$, you have to consider that $r$ s the distance to the point about you calculate the angular momentum and $\omega$ is the rate of change of the angle subtended by the fish about that same point. About what point is the problem asking you to find the angular momentum?

 

[haruspex]

Here's my calculation:
L = I*w = m*r^2*(v/r) = 0.5 * 11 * 3 = 16.5

Option (C) is close to my answer, but (A) is the official answer. Can anyone help, please? Thanks!

You got v/r from the equation $v=\omega r$, but what does the geometric relation of the directions of v and r need to be for that to be true?

 

[hidemi]

Thanks for all of your responses.
I tried my best to think it through, and here's what I got:
L = I w = m*r^2 * v/r = m * r * v = 0.5 * 1 *3 sin(30) = 3/4

The question is asking for the angular momentum of fish relative to the hand holding the fishing rod which is 1 meter for the 'r'. As for v, it has to be perpendicular to r, so it has to multiply by sin(30) to obtain the y component to be perpendicular to r.

 

[haruspex]

Thanks for all of your responses.
I tried my best to think it through, and here's what I got:
L = I w = m*r^2 * v/r = m * r * v = 0.5 * 1 *3 sin(30) = 3/4

The question is asking for the angular momentum of fish relative to the hand holding the fishing rod which is 1 meter for the 'r'. As for v, it has to be perpendicular to r, so it has to multiply by sin(30) to obtain the y component to be perpendicular to r.

The rod and fishing line are irrelevant. Just concentrate on the velocity of the fish and the straight line it is swimming along in relation to the hand.
What is the perpendicular distance from the hand to the line of movement of the fish?

 

[hidemi]

The rod and fishing line are irrelevant. Just concentrate on the velocity of the fish and the straight line it is swimming along in relation to the hand.
What is the perpendicular distance from the hand to the line of movement of the fish?

I calculated based upon your illustration and got the correct answer as below, but I'm not sure why.

L = I*w = 0.5 * 2^2 * 3/2 = 3

 

[haruspex]

I calculated based upon your illustration and got the correct answer as below, but I'm not sure why.

L = I*w = 0.5 * 2^2 * 3/2 = 3

Using the L=Iw form is not the simplest way to look at it. More natural here is the L=rmv form: linear momentum multiplied by perpendicular distance.
By differentiating wrt time you get the torque = force times perpendicular distance equation.

 

[hidemi]

Using the L=Iw form is not the simplest way to look at it. More natural here is the L=rmv form: linear momentum multiplied by perpendicular distance.
By differentiating wrt time you get the torque = force times perpendicular distance equation.

I got it. Thank you so much.