gem123456789
- 1
- 0
the given is 3mF is parallel to
11mF and 9mF in series connection and it is also parallel to
12mf and 6mf series connection
my answer to this is 1.17*10^-5 is this correct
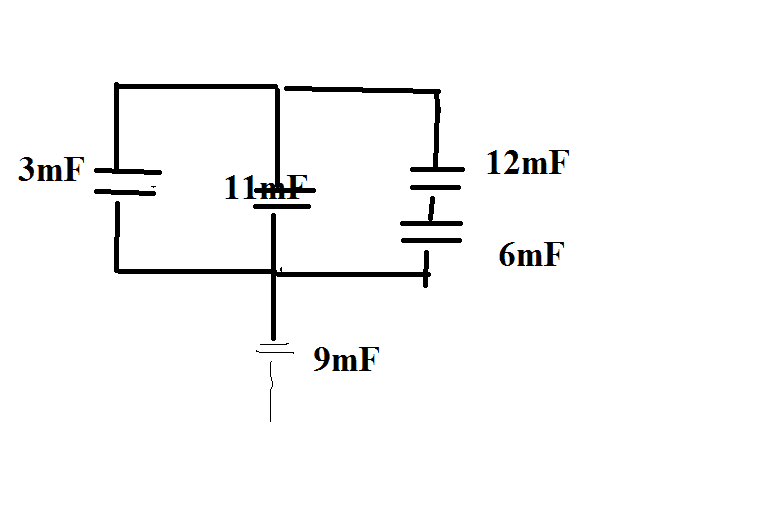
11mF and 9mF in series connection and it is also parallel to
12mf and 6mf series connection
my answer to this is 1.17*10^-5 is this correct
Last edited: