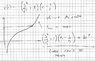- #1
binbagsss
- 1,254
- 11
Homework Statement
part d) from the following question please
Homework Equations
The Attempt at a Solution
[/B]
sol attached
So I see that the idea is that it is a maximum so to set ##\dot{r}=0## and then the maximum value is dependent on some values of J and K, to get the equation. But I'm totally confused as to :
- how we have showed it is attainable? (when would it not be attainable).
I've tried to look at my notes, and apologies for the length of the question this will add, but I'm just trying to compare and work out what to do. So my notes work with the Schwarzschild metric the following sketch:
with the following comments:
The behavior of the particle depends on the value of the energy K. For example, if K is such that the particle sits exactly at the bottom, then we have a circular orbit with radius rc (case A).If we now increase the energy a little bit, then r can vary, and we have a non-circular orbit. If we increase the energy still further, then its a bit different – it is no longer a bound orbit, instead theparticle comes in from infinity, comes up to a minimum radius rmin, and then goes out again; note there is no maximum r any more (case C)
Okay so in particular from this:
1) why is this called a minum radius , and it says there is no maximum. I understand that ##K## is such that it can only come up to this radius and no further, but I'm unsurre why you'd call it a minimum or a maximum.
2) the above question says an 'attainable maximum'. I thought perhaps the ideas where similar with the mimum radius for this one- there is no bound orbit, for some ##K## and ##J## as given by the equation above in the solution but here instead it is talking a 'maximum' radius. what is the difference? is it due to the shape of the potential?
is the comment 'cubic can't be solved ' relevant? if so, how?
quite stuck..many thanks for any help.