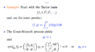You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
B GramSchmidt process for Taylor basis
AI Thread Summary
The discussion centers on the Gram-Schmidt process and its application to Taylor bases, emphasizing that the limits of integration depend on the chosen topological space and inner product definition. The interval [-1, 1] is highlighted as a sensible choice for Taylor series developed around x=0, but the basis can vary with different spaces. The necessity for orthonormal bases is acknowledged, with the inner product influencing the algorithm and resulting basis. It is clarified that the space must be defined first, as different spaces lead to different bases and integration limits. Understanding the specific Hilbert space in use is crucial for discussing the algorithm and integration boundaries.
Mathematics news on Phys.org
- 20,677
- 27,976
In the end it depends which topological space you consider and how the inner product is defined. Those two information set the conditions. As it is an example, we can simply consider ##L_2([-1,1])##. Taylor series are often developed around ##x=0##, so the choice of this interval makes some sense.
Somali_Physicist
- 117
- 13
This arrives at the legendary basis so It is abit fishy that it is a “coincidence “.So I could pic any numbers around 0?fresh_42 said:In the end it depends which topological space you consider and how the inner product is defined. Those two information set the conditions. As it is an example, we can simply consider ##L_2([-1,1])##. Taylor series are often developed around ##x=0##, so the choice of this interval makes some sense.
- 20,677
- 27,976
I haven't checked the algorithm. You might get additional scaling factors for your basis vectors by a different inner product, i.e. other spaces. Depends on whether you want to have a orthonormal or orthogonal basis.Somali_Physicist said:This arrives at the legendary basis so It is abit fishy that it is a “coincidence “.So I could pic any numbers around 0?
Somali_Physicist
- 117
- 13
I don’t believe that matters here, I just want to clarify why the limits were used and can we change them ad hocly.fresh_42 said:I haven't checked the algorithm. You might get additional scaling factors for your basis vectors by a different inner product, i.e. other spaces. Depends on whether you want to have a orthonormal or orthogonal basis.
- 20,677
- 27,976
As I said, the limits are determined by the space you consider, which again is determined by the elements and the inner product. You must now reason backwards. First is the space, then algorithm and at the end the basis. Another space results in another basis.Somali_Physicist said:I don’t believe that matters here, I just want to clarify why the limits were used and can we change them ad hocly.
Somali_Physicist
- 117
- 13
Ahh okay, well we want orthanormal bases, is it because of that we chose -1 to 1?fresh_42 said:As I said, the limits are determined by the space you consider, which again is determined by the elements and the inner product. You must now reason backwards. First is the space, then algorithm and at the end the basis. Another space results in another basis.
- 20,677
- 27,976
No. One possibility for an inner product for say, continuous functions on a real interval ##[a,b]## is e.g. ## \langle f,g \rangle = \int_a^b f(x)g(x)\,dx\,.## This determines how the algorithm is done and what basis finally drops out. You start with the Hilbert space which you want to consider, not the other way around. At the end of this article here https://www.physicsforums.com/insights/hilbert-spaces-relatives/ you can find some other examples. E.g. 5.10 is worth a look. There the integration is over the entire manifold. Of course in the above example we would get infinite integrals if we regarded ##\mathbb{R}## as our domain, so we need some restrictions on the allowed functions. But in general there is a variety of examples. As soon as you define and thus tell us, which Hilbert space you use, as soon can we talk about the algorithm and the borders of integration: different borders means different Hilbert spaces. So before the question even occurs, it has to be said, what we are talking about. I admit that this information isn't part of what you copied and in my opinion sloppy.Somali_Physicist said:Ahh okay, well we want orthonormal bases, is it because of that we chose -1 to 1?
Similar threads
- Replies
- 7
- Views
- 1K
- Replies
- 23
- Views
- 3K
- Replies
- 3
- Views
- 2K
- Replies
- 5
- Views
- 2K
- Replies
- 19
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 42
- Views
- 4K
- Replies
- 16
- Views
- 5K
Hot Threads
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
B What could prove this wrong? I'm having a dispute with friends
- Started by ducknumerouno
- Replies: 94
- General Math
-
B About a definition: What is the number of terms of a polynomial P(x)?
- Started by littlemathquark
- Replies: 48
- General Math
-
B How Many Straight Lines to Connect an N by M Array of Points in a Closed Loop?
- Started by bob012345
- Replies: 25
- General Math
-
B Geometry Puzzle with 20 points in a cross pattern
- Started by bob012345
- Replies: 31
- General Math
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math