jwxie
- 278
- 0
Given equation
f(x) = x^4 + 4x^3 - 2
so f ' (x) = 4x^3 + 12x^2
which simplified to
f ' (x) = 4x^2 (x+3), thus our critical points are 0 and -3
I will use this to sketch the curve
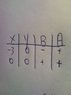
f ' (x) = 4x^2 (x+3)
Results are below.
According to my "sketch", the sequence is - , +, +, +
B means "before"
A means "after"
I used a very close number to generate this list
But I could not generate any sketch because (0,0) pair cannot have a +, +, + sequence. There must be a - sign, meaning the correct sequence should be -, +, -, +.
I need to hite (0,0) but there is no way as (-3,0) is increasing.
My calculator shows a different sequence. What is wrong with my sketch logic here?
f(x) = x^4 + 4x^3 - 2
so f ' (x) = 4x^3 + 12x^2
which simplified to
f ' (x) = 4x^2 (x+3), thus our critical points are 0 and -3
I will use this to sketch the curve
f ' (x) = 4x^2 (x+3)
Results are below.
According to my "sketch", the sequence is - , +, +, +
B means "before"
A means "after"
I used a very close number to generate this list
But I could not generate any sketch because (0,0) pair cannot have a +, +, + sequence. There must be a - sign, meaning the correct sequence should be -, +, -, +.
I need to hite (0,0) but there is no way as (-3,0) is increasing.
My calculator shows a different sequence. What is wrong with my sketch logic here?
Attachments
Last edited: