Jhenrique
- 676
- 4
Graphic Interpretation for Ʃf(x)Δx
Hello!
I was trying to understand what means:
\sum_{x_0}^{x_1}f(x)\Delta x
(when Δx = 1 and x ∈ Z, ie, a "discrete integration", topic very comun in discrete calculus).
I computed the result so:
\sum_{1}^{4}x^2\Delta x=\left [\frac{1}{3}x^3-\frac{1}{2}x^2+\frac{1}{6}x \right ]_{1}^{4}=F(4)-F(1)=14
and I sketched the graphic:
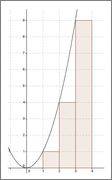
However, the Maple computes the result as:
\sum_{1}^{4}x^2\Delta x=>\sum_{1}^{4}x^2\cdot 1=>\sum_{1}^{4}x^2=30
Given a different result of calculated for me. Why?
Hello!
I was trying to understand what means:
\sum_{x_0}^{x_1}f(x)\Delta x
(when Δx = 1 and x ∈ Z, ie, a "discrete integration", topic very comun in discrete calculus).
I computed the result so:
\sum_{1}^{4}x^2\Delta x=\left [\frac{1}{3}x^3-\frac{1}{2}x^2+\frac{1}{6}x \right ]_{1}^{4}=F(4)-F(1)=14
and I sketched the graphic:
However, the Maple computes the result as:
\sum_{1}^{4}x^2\Delta x=>\sum_{1}^{4}x^2\cdot 1=>\sum_{1}^{4}x^2=30
Given a different result of calculated for me. Why?