nigels
- 36
- 0
In a trivial optimization problem, when seeking the value of x2 that minimizes y(x2)/(x2-x1), the solution is graphically given by the tangent line shown in the figure.
I'm having a lot of difficulty understanding why this is true, i.e., the logical steps behind the equivalence supporting the solution, either via calculus, algebraic, or geometric reasoning.
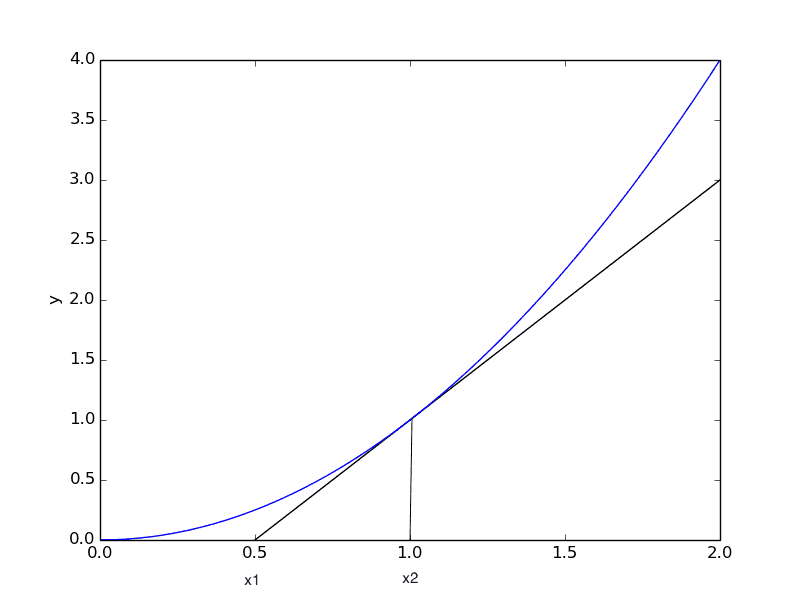
I'm having a lot of difficulty understanding why this is true, i.e., the logical steps behind the equivalence supporting the solution, either via calculus, algebraic, or geometric reasoning.