Graphing Eigenvectors and Sine Curves: Understanding the Relationship

[kostoglotov]

In my text, it tells me to find the eigenvectors of a 2nd difference matrix and graph the eigenvectors to see how they fall onto sine curves.

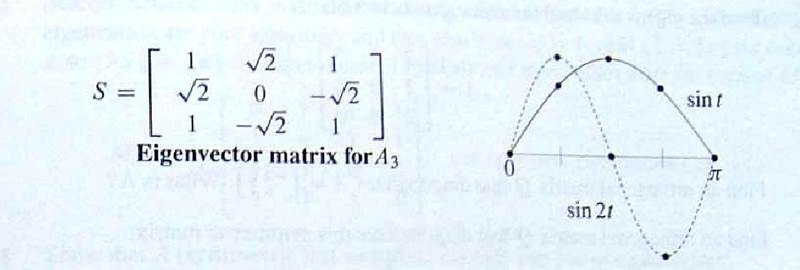
imgur link: http://i.imgur.com/oxbkTn6.jpg

My question is simple but general. What does this even mean? How did they produce this graph from the first two eigenvectors in the matrix on the left?

I tried in MATLAB to create an outer product of each vector with a time vector, but that plots straight lines.

 

[S.G. Janssens]

I'm not sure what a "2nd difference matrix is". Is it related to (a discretision of) the Laplacian?

The only thing that I can imagine at this moment is that the matrix $A$ is a representation of some operator acting on a vector space spanned by a basis of three harmonics. The eigenvectors of $A$ will then be coordinate vectors with respect to that basis. You can then "graph" an eigenvector by actually first computing the linear combination of basis harmonics to which it corresponds, and then graphing that linear combination (= a function).

 

[kostoglotov]

I'm not sure what a "2nd difference matrix is". Is it related to (a discretision of) the Laplacian?

The only thing that I can imagine at this moment is that the matrix $A$ is a representation of some operator acting on a vector space spanned by a basis of three harmonics. The eigenvectors of $A$ will then be coordinate vectors with respect to that basis. You can then "graph" an eigenvector by actually first computing the linear combination of basis harmonics to which it corresponds, and then graphing that linear combination (= a function).

Yeah the text gives no explication as to what it means to graph these vectors, and it's not mentioned in the video lectures. It's actually a really good course but Gilbert Strang is definitely an academic not a teacher. Still, I can't complain, it's an entire linear algebra course for free. :) And having an informal, messy text has hidden benefits, it forces you to get answers elsewhere, which is a better way of learning really.

 

[HallsofIvy]

Draw a short "arrow" showing the direction and length of the vector at that point on the graph.

 

[kostoglotov]

Draw a short "arrow" showing the direction and length of the vector at that point on the graph.

But the vectors have three elements, and are being graphs in 2 dimensions.

 

[HallsofIvy]

But the vectors have three elements, and are being graphs in 2 dimensions.

You've never heard of two-dimensional vectors?

 

[kostoglotov]

You've never heard of two-dimensional vectors?

Wow, ok, one last shot...how would I graph $[1,\sqrt{2},1]$ on a 2 dimensional plane? I've not seen how to do that before, but ok.

 

[S.G. Janssens]

@kostoglotov : Are you sue these vectors aren't coordinate vectors with respect to some basis consisting of three functions? That is namely what the function graphs suggested to me.

 

[kostoglotov]

@kostoglotov : Are you sue these vectors aren't coordinate vectors with respect to some basis consisting of three functions? That is namely what the function graphs suggested to me.

Very possibly, the second difference matrix seems to be a matrix for the second finite difference, in a diff eqs section.

Thing is, it's possible I've followed the curriculum in the wrong order, because I haven't seen anything like this up until now. Maybe I should have done the later section on Fourier Transforms before getting to where I am now, since the syllabus skips around a bit.

Here is the entire problem:

imgur link: http://i.imgur.com/EGO4q9D.jpg

and a bit more of the solution:

imgur link: http://i.imgur.com/zBOhs0n.jpg

 

[vela]

I think this is what they're doing in the solution. If you divide S by $\sqrt 2$, you get
$$S/\sqrt{2} = \begin{bmatrix} 1/\sqrt{2} & 1 & 1/\sqrt{2} \\ 1 & 0 & -1 \\ 1/\sqrt{2} & -1 & 1/\sqrt{2} \end{bmatrix}.$$ The points marked on $\sin t$ correspond to the first row of this matrix. That is, evaluate $\sin t$ at $t = \pi/4, \pi/2, 3\pi/4$ and you get the values in the first row. Similarly, the points marked on $\sin 2t$ correspond to the second row.