Undergrad Graphs of inverse trigonometric vs inverse hyperbolic functions

[Happiness]

I noticed the graphs of $y=\cos^{-1}x$ and $y=\cosh^{-1}x$ are similar in the sense that the real part of one is the imaginary part of the other. This is true except when $x<-1$ where the imaginary part of $y=\cos^{-1}x$ is negative but the real part of $y=\cosh^{-1}x$ is positive.

I believe whether they are positive or negative is by a choice of convention. So why don't we define them to be both positive or both negative?

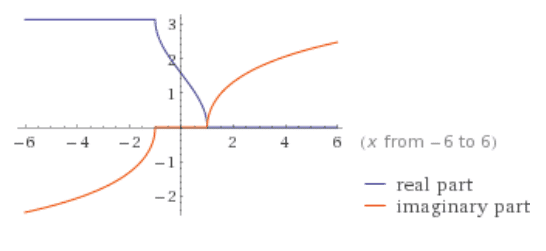
$\cos^{-1}x$ graph: http://www.wolframalpha.com/input/?i=y=acos(x)

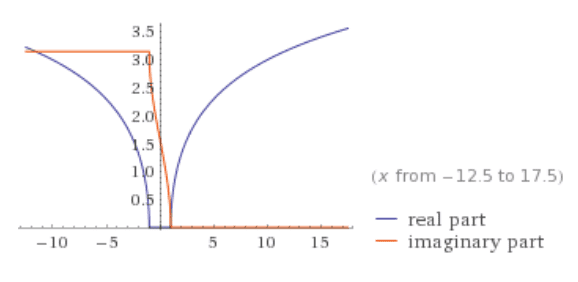
$\cosh^{-1}x$ graph: http://www.wolframalpha.com/input/?i=y=acosh(x)

Question 2:
Since the real part of $\cosh^{-1}x$ is the imaginary part of $\cos^{-1}x$ when $x>1$, this means that multiplying $i$ to the real part of $\cosh^{-1}x$ gives the imaginary part of $\cos^{-1}x$:
$i\cosh^{-1}x=\cos^{-1}x$ for $x>1$.

Similarly, since the real part of $\cos^{-1}x$ is the imaginary part of $\cosh^{-1}x$ when $x<1$, we have
$\cosh^{-1}x=i\cos^{-1}x$ for $x<1$.

We have two rules depending on the value of $x$. Why not use the same rule? And change the definition of $\cosh^{-1}x$ accordingly: define the real part of $\cosh^{-1}x$ as negative for $x>1$.

 

[Buzz Bloom]

Hi Happiness:

If your reasoning is the based on the graphs, you need to understand that those graphs are not complete.

Given a graph of y = f(x), you can get the inverse graph x = f^-1(y) by reflecting the graph about the main diagonal y=x. As an example, consider the graphs for y = x² and x = √y . When you show a graph for x = √y it is comon to ignore the values for negative x, but the negative values are actually part of the graph. x has both + and - values for a given value of y.

Regards,
Buzz