MHB Graphs of Negative Fractional Powers x^(-p/q)

AI Thread Summary
The discussion focuses on understanding the graphs of negative fractional powers, specifically x^(-p/q). The value of p/q significantly influences the shape and behavior of the graph, affecting both the domain and range. The domain is defined by the conditions where the function is valid, often excluding values that make the denominator zero or violate square root conditions. The range can be more complex to determine but can often be estimated based on the function's behavior. Asymptotes are identified by analyzing the limits of the function as it approaches critical points, such as the zeros of the denominator.
confusedatmath
Messages
14
Reaction score
0
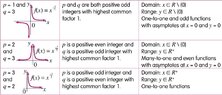
Can someone explain how these graphs are drawn. How does the value of p/q affect this graph? How does the domain and range change? How are the asymptotes found?

The below is an image about what I'm talking about:

View attachment 1831

Here is a question the deals with this type of graph (no idea how to solve it because I'm unfamiliar with these kind of graphs)

View attachment 1832
 

Attachments

  • q1a.jpg
    q1a.jpg
    45.6 KB · Views: 158
  • q1b.jpg
    q1b.jpg
    16.4 KB · Views: 114
Mathematics news on Phys.org
Think about the domain as where the function is defined. For example, if you think of a fraction with a polynomial in the denominator then it it is defined for all numbers except for the zeros of this polynomial. If you have a square root then it has to be defined for only positive integers. If you have both then you have to take care of both conditions. As for the range it is a little bit tricker to work with but for the most time you can guess it.

Take the following example

$$f(x)=\frac{1}{x+a}$$

What is the domain, range and horizontal and vertical asymptotes ?
 

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Thread 'Non-orthogonal bases'

Suppose ,instead of the usual x,y coordinate system with an I basis vector along the x -axis and a corresponding j basis vector along the y-axis we instead have a different pair of basis vectors ,call them e and f along their respective axes. I have seen that this is an important subject in maths My question is what physical applications does such a model apply to? I am asking here because I have devoted quite a lot of time in the past to understanding convectors and the dual...
View full post »
Thread 'Imaginary Pythagoras'

Thread 'Imaginary Pythagoras'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Similar threads

MHB Graphs of Functions with fractional powers x^(p/q)
Replies
2
Views
2K
MHB Discontinuity: Point discontinuity
Replies
8
Views
5K
MHB Fractions/brackets/parentheses and powers.
Replies
3
Views
3K
Is it possible to define irrational powers for negative numbers?
Replies
2
Views
3K
I Electric Potential in circuit
Replies
3
Views
1K
Why is the electric force the negative of the position derivative of EPE?
Replies
5
Views
1K
MHB Finding the intersection points on the graph y=sinx, y=cosx and y=tanx
Replies
4
Views
9K
MHB F(x) is non negative for all real x
Replies
9
Views
3K
Help with handling fractional powers in equations
Replies
9
Views
5K
I ##(A/\mathfrak{a})_{\mathfrak{p}/\mathfrak{a}}## and its isomorphism?
Replies
31
Views
1K

Hot Threads

Recent Insights

Back
Top