Grating and slits problem 28 from 9702_s17_qp_13.pdf

[Michael Marchenko]

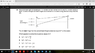
I can exclude B because B shows maxima, but I do not know how to exclude A and D.

These are the equations for the diffraction grating and the double-slit experiment:

dSin(A) = nL

DL = ax

It seems that this problem is about the combination of both.

C is probably the correct answer.

https://physics18.weebly.com/uploads/5/9/8/5/59854633/9702_s17_qp_13.pdf
https://physics18.weebly.com/uploads/5/9/8/5/59854633/9702_s17_ms_13.pdf

 

[Charles Link]

For $A$, what do you get if $n$ is even? $\\$ Editing: The answers really needs absolute value signs and should be written $|S_2P-S_1P|=...$ Then it will work for the $nth$ dark fringe counted from the center up or down. To determine whether the correct answer is $C$ or $D$, what do you get for the first ($n=1$) dark fringe (up or down) from the center? Does it obey $C)$ $|S_2P-S_1P|=(1/2) \lambda$, or $D)$ $|S_2P-S_1P|=(3/2) \lambda$? $\\$ Additional item: Please use the homework template in the future for your homework problems.