Gravitational force of three objects on a fourth

[coneheadceo]

Homework Statement

Four spheres of equal 9.5 kg are located at the corners of a square of length 0.6 m per side. Find the magnitude and direction of the gravitational field on one by the other three spheres

Homework Equations

gravity = GM/r^2 with G = gravitation constant, M = mass, r = radius

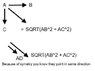
The field strength of the diagonal mass = GM/(r*.71)^2
The sum of the field magnitudes from the two neighbored masses is GM(.71)/r^2
The total magnitude = GM/((2r)^2) + GM(.71)/r^2

The Attempt at a Solution

So to clarify the ".71" is the sin of 45°, the radius of the neighboring spheres is .6 m and using phythagorean the diagonal radius is .85 m.

Solving... the answer in the book says...3.2 x 10^-8 N but...

(6.67x 10^-11)(9.5)/(2 * 0.6)^2 + (.71)(6.67x10^-11)(9.5)/(.85)^2=

4.4x10^-10 + 6.2x10^-10 = 1.06 x 10^-9

Where do I need to be set straight? Wrong equation(s) or substitutions?

 

[gabbagabbahey]

The field strength of the diagonal mass = GM/(r*.71)^2
The sum of the field magnitudes from the two neighbored masses is GM(.71)/r^2
The total magnitude = GM/((2r)^2) + GM(.71)/r^2

The gravitational field is a vector field. This is not how you find the magnitude of a sum of vectors (unless they all point in the same direction).

||\mathbf{A}+\mathbf{B}|| \neq ||\mathbf{A}||+||\mathbf{B}||

 

[coneheadceo]

So do I just use
F = (G*m1*m2)/r^2 for each sphere at 90° and

F = sin 45°(G*m1*m2)/r^2 for the diagonal sphere and add them all together?

doing that I get 3.9 x 10^-8

 

[CWatters]

Forget the one on the diagonal for the moment... Go look up how you add two vectors that are at right angles.

 

[coneheadceo]

You would use pythagorean method...

A-----B
| /
| /
C-----D
so let's say we call "A" sphere that is the 4th sphere... calculating the force of gravity between A and B would give a result of

1.67*10^-8

using g = G (m1m2/r^2)

and the same for A - C

using pythagorean theorm... c^2 = a^2 + b^2 gives us a "g" between A-D of 2.4x 10^-8

am I on the right track now? if so then do I add these together or am I waaaay off.

btw ABCD is supposed to be a square but I can't seem to get the dash to move over.

 

[CWatters]

Yes that right.

and since it's a square the resulting vector of the first two points at the third sphere making it easier to add the effect of that one.

 

[coneheadceo]

Now I'm confused since the answer in the book is 3.2x10^-8

adding 2.4 + 1.67 +1.67 =5.74 x10^-8

 

[CWatters]

Total force = SQRT{(Force between A&B)² + (Force between A&C)²} + (Force between A&D)

and it points from A to D.

You appear to have calculated SQRT{(Force between A&B)² + (Force between A&C)²} correctly. I make that part = 2.36 * 10^-8

It's the (Force between A&D) you appear to have wrong. The book answer appears to be correct.

Aside: Strictly speaking the equation I provide should be vector addition but you can simplify it to ordinary addition because we know that the result of adding two of the forces results in an vector that points in the same direction as the third.

 

[CWatters]

Might help. Work out what force AD is. Then add it to the 2.36 * 10^-8 you calculated. Remember D is further away from A.

 

[gabbagabbahey]

You should really just choose an appropriate coordinate system and break down each of the 3 forces into their components in that coordinate system. As long as the basis vectors in the coordinate system you choose are orthogonal to each other (like Cartesian unit vectors), you can then just add the components together.

In 2D Cartesian coordinates, for example the sum two vectors (\mathbf{A} = A_x \mathbf{e}_{x} + A_y \mathbf{e}_{y} and \mathbf{B} = B_x \mathbf{e}_{x} + B_y \mathbf{e}_{y}) is computed as follows:

\mathbf{A} + \mathbf{B} = (A_x +B_x)\mathbf{e}_{x} + ( A_y + B_y ) \mathbf{e}_{y}

And so the magnitude of the resulting vector is just ||\mathbf{A} + \mathbf{B} || = \sqrt{(A_x +B_x)^2 + (A_y +B_y)^2}.

This is something that you will find in any introductory linear algebra textbook, and is usually taught in high school physics. If you are having this much difficulty adding three vectors together and finding the resultant vector's magnitude and direction, you really need to go back to your textbook (or look up vector addition online) and re-read the section on adding vectors and study the examples in the textbook.

 

[coneheadceo]

Thank you CWatters! And yes Gab... I am taking a college level intro physics course with an "okay" book. It's been 15 years since I've worked with Physics like this and I'm going to have to review more before diving in. I would have been okay with three objects but four is a bit of a stretch.

 

[CWatters]

Its even longer since I did it.

Gab's answer is better than mine because next problem will have unequal masses and the cheat/trick I used won't work. As he said best work out the components of all the vectors in a suitable co-ordinate system and add them up.