Gravitational Time Dilation - Confused

[valdar]

Hey everyone, recently I watched a discovery program about time travel. I understood time travel from the view point of traveling at/close to the speed of light, however, I am completely confused as to how time travel is possible using gravity.

I know that it has to do with gravitational potential, but under that logic, one could say that as gravity increases, so does the speed at which objects fall, ergo, making them age slower. (Assuming that objects can fall at/close to the speed of light)

I just don't understand the whole concept of Gravitational Time Dilation, can anyone please shed some light on it?

 

[tiny-tim]

Welcome to PF!

Hey valdar! Welcome to PF!

Hey everyone, recently I watched a discovery program about time travel. I understood time travel from the view point of traveling at/close to the speed of light, however, I am completely confused as to how time travel is possible using gravity.

It isn't!

Using wormholes possibly, using gravity definitely not.

 

[yuiop]

Hey everyone, recently I watched a discovery program about time travel. I understood time travel from the view point of traveling at/close to the speed of light,

First it should be made clear that the "time travel" when traveling at close to the speed of light is just the relative slowing of the moving clock relative to the clock of a stationary observer. There is no going backwards in time and murdering you grandparents or whatever else time travellers have the urge to do. There is no changeing the order of a sequence of events that have already happened (causalty). There is just differential ageing.

however, I am completely confused as to how time travel is possible using gravity.
I know that it has to do with gravitational potential, but under that logic, one could say that as gravity increases, so does the speed at which objects fall, ergo, making them age slower.

Although the speed of a falling clock does have some influence on the slow down of the proper time of the falling clock it is not the crux of the matter. A perfectly stationary clock low down in a gravitational potential well, runs slow relative to clock higher up.

(Assuming that objects can fall at/close to the speed of light)

Yes, they can. An object released from infinity aproaches the local speed of light as it aproaches the event horizon of a black hole. From the point of view of an observer higher up the velocity of the falling object (and the coordinate speed of light) aproaches zero as it aproaches the event horizon.

I just don't understand the whole concept of Gravitational Time Dilation, can anyone please shed some light on it?

There is a lot of ground to cover here and I have a feeling this is going to be a long thread. You can get started by googling the "equivalence principle".

 

[valdar]

Thank you for replying. My biggest spheel is the following:

https://www.physicsforums.com/showpost.php?p=1320213&postcount=4

as they rise from the centre to the surface, lose kinetic energy.

but as they fell from the surface to the centre, they gained kinetic energy

The vary same photons that ended up being "decelerated" while moving from the clock to the observers eye are "accelerated" when they move from a light source (lets say at the same distance as the observer themselves) to the clock.

So if the distances are the same, the deceleration is equal to the acceleration, there shouldn't be any shifts. Where am I wrong?

 

[yuiop]

Thank you for replying. My biggest spheel is the following:

https://www.physicsforums.com/showpost.php?p=1320213&postcount=4

but as they fell from the surface to the centre, they gained kinetic energy

The vary same photons that ended up being "decelerated" while moving from the clock to the observers eye are "accelerated" when they move from a light source (lets say at the same distance as the observer themselves) to the clock.

So if the distances are the same, the deceleration is equal to the acceleration, there shouldn't be any shifts. Where am I wrong?

You would be right if the source of the photons in George's hole was a torch in the hand of the observer at the top of the hole. On the way down to the clock at the bottom of the hole they gain energy (higher frequency) and then after being reflected off the bottom clock they would lose the same amount of energy and arrive back at the top with the same frequency that they were emitted with. I think in George's example the clock is the source of the photons. (Imagine the hands painted with glow in the dark luminous paint)

 

[valdar]

Sorry for the double post, but I --THINK-- I get it.

Let's say you have a room. In that room you have a ball bouncing between the two walls. Every bounce is one second.

You get two of the rooms. You put one room on Earth's surface, and another in the centre of the earth.

For the room at the surface, the balls bounce is accelerated by gravity.
For the room at the centre, the balls bounce is not accelerated by gravity.

Observing the centre balls bounces from the surface, it will seem slower, and vice versa, is this about right?

 

[FunkyDwarf]

*thumbs up* except with light its not about physical acceleration but rather a path difference caused by curved space time. Also a freqency change (gravitational redshift). But it has much the same effect, in this example.

 

[yuiop]

Sorry for the double post, but I --THINK-- I get it.

Let's say you have a room. In that room you have a ball bouncing between the two walls. Every bounce is one second.

You get two of the rooms. You put one room on Earth's surface, and another in the centre of the earth.

For the room at the surface, the balls bounce is accelerated by gravity.
For the room at the centre, the balls bounce is not accelerated by gravity.

Observing the centre balls bounces from the surface, it will seem slower, and vice versa, is this about right?

It doesn't just seem slower, it IS slower. The slow down is not due to lack of being accelerated by gravity either. Imagine the balls are "super balls" that lose no energy with each bounce and they are bouncing from side to side horizonatally so that gravity has no direct influence on its bounce speed. A digital device counts each bounce of the balls. When one of the ball rooms is lowered to the centre of Earth and and brought slowly back to the surface again, the room that was at the centre would have counted less bounces, but both balls will be bouncing at the same speed when back together at the surface.

 

[valdar]

Ok then there is another issue.

Not being in a gravity field makes your internal clock run slower.THIS POINT IS WRONG. Being in the middle of a strong field makes your internal clock run slower
Traveling at the speed of light makes your internal clock run slower.

The faster you go the more you weigh, the more you weigh the more mass you have, making you, yourself have a gravitational field. But then how are you both able to have your internal clock run slow due to traveling fast, but at the same time, have it run fast by being the creating factor of a gravity field?

 

[sylas]

Ok then there is another issue.

Not being in a gravity field makes your internal clock run slower.
Traveling at the speed of light makes your internal clock run slower.

Um... it is the clock that is deep inside a gravitational field that runs more slowly.

There's a great story on the web of a scientist-dad who took his kids on a camping trip up the mountains, along with some atomic clocks. See Clocks, Kids, and General Relativity on Mt Rainier. Just because I think the pictures are hilarious, here's a shot of plan A: backpack your atomic clock, compared with plan B: use the car and drive up a mountain.

(<-- Plan A. Plan B -->)

They used plan B, and also left some clocks back home for the subsequent comparison.

The clocks up the mountain run faster. By going up the mountain with his kids, this Dad got to spend an extra 22 nanoseconds with his kids that he'd have missed by staying home. As he says: It was the best extra 22 nanoseconds I've ever spent with the kids.

The faster you go the more you weigh, the more you weigh the more mass you have, making you, yourself have a gravitational field. But then how are you both able to have your internal clock run slow due to traveling fast, but at the same time, have it run fast by being the creating factor of a gravity field?

Actually, the faster you go, the more energy you have ... as measured by someone who remains at rest! For you, in motion, there's no extra energy or extra gravity, involved.

Cheers -- Sylas

 

[valdar]

Um... it is the clock that is deep inside a gravitational field that runs more slowly.

Actually, the faster you go, the more energy you have ... as measured by someone who remains at rest! For you, in motion, there's no extra energy or extra gravity, involved.

Cheers -- Sylas

From an outside observer, you would be in the middle of a gravitational well, traveling at close to the speed of light then, right?

If so, then that's what I was looking for.

Wow the world is really subjective than I originally thought

 

[JesseM]

From an outside observer, you would be in the middle of a gravitational well, traveling at close to the speed of light then, right?

Why do you say you'd be traveling at close to the speed of light? In the most common coordinate system to use for spherical bodies like planets (Schwarzschild coordinates), if you're at a constant distance from the center then your speed is zero.

 

[valdar]

Why do you say you'd be traveling at close to the speed of light? In the most common coordinate system to use for spherical bodies like planets (Schwarzschild coordinates), if you're at a constant distance from the center then your speed is zero.

Sorry, let me explain that better, my original question was that as a mass accelerates, its weight increases, with an increase in weight there would be an increase in gravitational pull towards the object.

Originally I had a mistake in my assumptions. Correctly, an object traveling very quickly would be both deep in a gravitational well (due to its own increase in mass, gravity) and it would have time pass by slower, and due to the fact that it is traveling close to the speed of light, it would also have time pass by slower.

 

[sylas]

From an outside observer, you would be in the middle of a gravitational well, traveling at close to the speed of light then, right?

I don't think so; the association of gravity and the additional energy of a moving object is not that simple. In fact, special relativity works all by itself in your example.

If you have a clock on a massive object (large rest mass) which is moving (relative to you) at near to light speed, then there are two components in the time difference: the velocity part, that can be obtained with special relativity, and the gravitational part, for which you need general relativity.

Wow the world is really subjective than I originally thought

Indeed! It's worth mentioning, however, that rest mass is not subjective. It is an invariant.

If you have two observers moving relative to each other at high speed, then their observations are symmetrical. From the perspective of either one, the other clock is slower.

This symmetry is broken if one of the observers shifts their inertial frame, by changing velocity, and that's why there's no actual paradox with any of the traveling twins variations.

In the case of gravitational time dilation, there's no symmetry between the observers. Each observer agrees that the clock in the kitchen is deeper into a gravitational field and running more slowly than the clock up on Mt Rainer. You can have observers on the mountain, and in the kitchen at home, in direct communication with each other, and agreeing without ambiguity that the kitchen clock runs slow.

Cheers -- Sylas

 

[valdar]

If you have a clock on a massive object (large rest mass) which is moving (relative to you) at near to light speed, then there are two components in the time difference: the velocity part, that can be obtained with special relativity, and the gravitational part, for which you need general relativity.
Cheers -- Sylas

This was what I was trying to get at.

Thank you :)

 

[valdar]

From the information in this thread, I think the conceptualized spacetime material is actually drawn wrong.

An "Empty" (objectless) area of space is has no gravity exerted upon it (minute, but very close to 0).
The centre of any object in space (Excluding black holes) has no gravity exerted upon it either.

If gravity is the culprit that bends the spacetime continuum, shouldn't it be equal between the core of an object, and empty space?

see the attached picture - Please excuse my terrible MS paint skills

 

[sylas]

From the information in this thread, I think the conceptualized spacetime material is actually drawn wrong.

An "Empty" (objectless) area of space is has no gravity exerted upon it (minute, but very close to 0).
The centre of any object in space (Excluding black holes) has no gravity exerted upon it either.

If gravity is the culprit that bends the spacetime continuum, shouldn't it be equal between the core of an object, and empty space?

see the attached picture - Please excuse my terrible MS paint skills

No, the conventional picture is the one that is more correct.

You can show this by thinking of the gravitational blue shift of a light of a fixed reference frequency being shined down a deep hole to a detector at the center of the Earth.

There is a blue shift observed when you shine the light down the height of the tower at Harvard. Put another way; the atomic clock at the top of the tower is running faster than the one at the bottom.

Now imagine digging into the basement. Do you think there will be more, or less blueshift observed?

There will be more blueshift observed, of course; and that's true because the light is moving deeper into the gravitational well. So it goes, all the way down to the center.

This is getting back to being subjective again. A clock at the center of the Earth runs more slowly than one at the surface. You figure out how much more slowly NOT by measuring the gravitational acceleration in each location; but by considering a world line between the two locations... which involves moving deeper and deeper into a gravitational well.

Cheers -- sylas

 

[valdar]

From your example, there is a specific distance between the top and bottom of the tower. During that distance there is a specific amount of gravity excreted.
If you dig into the basement, more gravity is excreted (due to increase in distance), increasing the blue shift.

If you dig deep enough, gravity will become weaker and weaker, decreasing the -amount- that the blue shift happens by.

It will still happen, it will still increase, but at a less and less value, which will be 0 at the centre then?

Is that right?

 

[sylas]

From your example, there is a specific distance between the top and bottom of the tower. During that distance there is a specific amount of gravity excreted.
If you dig into the basement, more gravity is excreted (due to increase in distance), increasing the blue shift.

If you dig deep enough, gravity will become weaker and weaker, decreasing the -amount- that the blue shift happens by.

It will still happen, it will still increase, but at a less and less value, which will be 0 at the centre then?

Is that right?

Yes, I believe so. That is, the rate of change of blue shift goes to zero at the center of the Earth. But it's more and more blue shift all the way down.

Inside a large hollow cavity at the center of the Earth, observers distributed around the cavity would all see their clocks running at the same rate, and they would all see the same difference between their clock, and a clock at the surface.

Cheers -- sylas

 

[A.T.]

From your example, there is a specific distance between the top and bottom of the tower. During that distance there is a specific amount of gravity excreted.
If you dig into the basement, more gravity is excreted (due to increase in distance), increasing the blue shift.

If you dig deep enough, gravity will become weaker and weaker, decreasing the -amount- that the blue shift happens by.

It will still happen, it will still increase, but at a less and less value, which will be 0 at the centre then?

Is that right?

Yes, there was a recent thread about this:
https://www.physicsforums.com/showthread.php?t=308904

Gravitational time dilation is not a local effect, but a clock rate ratio between two distant points in space. It is determined by the spacetime curvature between the two points, and can occur even if spacetime is locally flat at both points.

 

[yuiop]

From your example, there is a specific distance between the top and bottom of the tower. During that distance there is a specific amount of gravity excreted.
If you dig into the basement, more gravity is excreted (due to increase in distance), increasing the blue shift.

If you dig deep enough, gravity will become weaker and weaker, decreasing the -amount- that the blue shift happens by.

It will still happen, it will still increase, but at a less and less value, which will be 0 at the centre then?

Is that right?

Nope, it's wrong. Gravitational time dilation is not as closely connected to gravitational acceleration as you think and has more to do with gravitational potential. For example a clock at the centre of the Earth will be running slower than a clock at the centre of the Moon because the Earth has more mass and is in a deeper gravitational well. You can think of the rubber sheet analogy. A large bowling ball representing the Earth puts a deeper dent (gravitational well) in the rubber sheet than the dent made by a cricket ball representing the Moon. The gravitational acceleration at the centre of the Earth and at the centre of the Moon is the same (zero) but the clocks at the centres of the two bodies are NOT running at the same rate. The blue shift is increasing the deeper you go and the larger the mass of the body and does NOT go towards zero. If the body is sufficiently massive and its mass has collapsed towards a radius of 2GM/c^2 then a clock at the centre will stop (and the blue shift become infinite.) as the body becomes a black hole. That is the limiting case.

<EDIT> I think I have misinterpreted your statement above. My statement above is more applicable to this earlier statement of yours:

An "Empty" (objectless) area of space is has no gravity exerted upon it (minute, but very close to 0).
The centre of any object in space (Excluding black holes) has no gravity exerted upon it either.

If gravity is the culprit that bends the spacetime continuum, shouldn't it be equal between the core of an object, and empty space?

The time dilation at the core of an object is not equal to the time dilation of empty space.

 

[valdar]

Look at it this way, if you have a stationary massive object in space with a tunnel (from one end to the other) in the middle of it, say a planet. As the light is traveling down the tunnel it is blue shifted until the centre of the object. From the centre of the object to the other side of the tunnel the light is red shifted, overall, there would be no shift, would there?

See the attached image.2nd part. I understand that in the centre of the Earth a clock would run slower than on the surface, how come?

Gravitational time dilation is not a local effect, but a clock rate ratio between two distant points in space. It is determined by the spacetime curvature between the two points, and can occur even if spacetime is locally flat at both points.

So then the speed of time is measured by how high or low we are on the spacetime continuum? relatively speaking of course.

 

[sylas]

Look at it this way, if you have a stationary massive object in space with a tunnel (from one end to the other) in the middle of it, say a planet. As the light is traveling down the tunnel it is blue shifted until the centre of the object. From the centre of the object to the other side of the tunnel the light is red shifted, overall, there would be no shift, would there?

That's correct. But remember, any "shift" is always dependent on an observer; not an absolute property of the light.

You can only say the light coming out of the tunnel is "redshifted" as a comparison between what is observed in the center, and what is observed half way out.

2nd part. I understand that in the centre of the Earth a clock would run slower than on the surface, how come?

Because that's how massive objects bend spacetime.

So then the speed of time is measured by how high or low we are on the spacetime continuum? relatively speaking of course.

I don't think that's a meaningful statement, as phrased. "high and low on the spacetime continuum"?

The passage of time is measured by clocks. A clock has a "world line", and "proper time" along a world line is what is measured by a clock with that world line. Relativity is the theory that allows you to infer what will be measured by a clock, given its world line.

Cheers -- sylas

 

[valdar]

That's correct. But remember, any "shift" is always dependent on an observer; not an absolute property of the light.

In the above example, as drawn out in MS paint, how would you see the light shifted inside the planet? you see the light leave a source, travel into, and through the planet, and then out the other side... what would you see happen? wouldn't you see both shifts

wait... in order for you to see both shifts that means that at every point in time during that line light is given off from that line which then travels towards you. wow. based on that youd see something completely different.

That didn't work. Let's say that you are measuring the blue/red shifts of light. One measuring device is located at the beginning (before the blue shift) one in the middle (when the blue shift becomes red shift) and at the end (at the end of the red shift). In that case wouldn't you be able to "sense" the shifts using the measuring tools?

I don't think that's a meaningful statement, as phrased. "high and low on the spacetime continuum"?

The passage of time is measured by clocks. A clock has a "world line", and "proper time" along a world line is what is measured by a clock with that world line. Relativity is the theory that allows you to infer what will be measured by a clock, given its world line.

Cheers -- sylas

Meaning, clocks only measure how high we are in the spacetime continuum, in other words if we are on a heavy object, or not. At a high point on the continuum clocks would run at a specific speed, at a low point they would run at another one, how far off am i?

 

[yuiop]

In the above example, as drawn out in MS paint, how would you see the light shifted inside the planet? you see the light leave a source, travel into, and through the planet, and then out the other side... what would you see happen? wouldn't you see both shifts

No single observer would be able to see the entire light path and all the shifts. You would require a series of observers arranged along the path. Imagine the test beam is wide and they have small detectors that can sample the beam without blocking it. Later they can compare measurements and compare them with what GR predicts. Using the calculations of GR they can predict what they would measure at some point they have not yet tested and then check if the prediction is correct. After predicting and checking that the equations are correct for several random points they can build up confidence in the predictions and determine what the frequency is at any point using only maths without requiring an infinite number of observers. Oh, and yes they would see both shifts.

That didn't work. Let's say that you are measuring the blue/red shifts of light. One measuring device is located at the beginning (before the blue shift) one in the middle (when the blue shift becomes red shift) and at the end (at the end of the red shift). In that case wouldn't you be able to "sense" the shifts using the measuring tools?

Yes, as above.

Meaning, clocks only measure how high we are in the spacetime continuum, in other words if we are on a heavy object, or not. At a high point on the continuum clocks would run at a specific speed, at a low point they would run at another one, how far off am i?

continuum is a vague word. If you mean that at a high gravitational potential clocks run faster relative to clocks at a low gravitational potential... then yes.

2nd part. I understand that in the centre of the Earth a clock would run slower than on the surface, how come?

Science has very few answers for why the universe is the way it is or how it works the way it does (what mechanism). It can only tell you what you would expect to measure given certain parameters and offer some guiding principles learned from observation and experience. One of those guiding principles in GR is the equivalence principle and another is the constant speed of light as measured locally.

So we can not say WHY clocks in at a low gravitational potential run slower than clocks at higher gravitational potential anymore than we can state WHY objects fall from a high potential to a low potential. (not yet anyway without a complete gravitational theory of everything). There is some connection between the two observations and it might be possible to claim at some level that objects fall from a high gravitational potential to a lower gravitational potential because time runs slower at lower gravitational potential (or vice versa).

When studying relativity you have to careful to note when you are talking about relative or coordinate or local or proper measurements. For example the statement that the speed of light is always constant is only true if you only mean the local speed of light. The statement that clocks run at different speeds is only true if you mean the relative rate rather than the proper rate. The proper rate of a clock is always one second per second but to claim that clocks do not run at different rates without making it clear that you specifically mean only proper clock rates is misleading just as it is misleading to claim the speed of light is always constant without making it clear you are only talking about the local speed of light. As you go deeper into a gravity well the relative speed of light gets slower, the relative speed of clocks gets slower and the relative length of rulers get shorter and the consequence of all that is that any observer always measures the local speed of light to be the same.

Another surprise is that the frequency of a rising photon does not actually change! The observer higher up with the faster clock measures the frequency of the light as decreasing, merely because he is making the measurement with a faster clock! When you think about it, it makes sense. The energy of a photon is determined by its frequency. If its frequency was really getting lower then you have to ask where has all the missing energy gone? Objects usually shed energy by emitting photons, but photons do not shed energy by emitting more photons. Another mechanism used in Newtonian physics is that objects give up there energy to a gravitational field but in GR the gravitational field is not considered to store energy in the classical way. Therefore a rising or falling photon neither gains nor loses energy, but locally it appears to.

 

[DrGreg]

Another surprise is that the frequency of a rising photon does not actually change! The observer higher up with the faster clock measures the frequency of the light as decreasing, merely because he is making the measurement with a faster clock! When you think about it, it makes sense. The energy of a photon is determined by its frequency. If its frequency was really getting lower then you have to ask where has all the missing energy gone? Objects usually shed energy by emitting photons, but photons do not shed energy by emitting more photons. Another mechanism used in Newtonian physics is that objects give up there energy to a gravitational field but in GR the gravitational field is not considered to store energy in the classical way. Therefore a rising or falling photon neither gains nor loses energy, but locally it appears to.

I'm afraid that doesn't really make sense. The only frequency a photon has is the frequency an observer measures with a clock. Different observers measure different frequencies, so to say "the frequency stays the same" is wrong if two observers measure different frequencies at different heights. Frequency is an observer-dependent concept, as are time, distance, energy, etc. If two different inertial observers measure different energies there's no need to explain where the energy has gone because they are measuring in different frames.

And if you choose to measure a rising photon at two different heights in a single accelerating frame, the photon's loss of energy (gravitational red-shift) is accounted for as a gain in potential energy. (That logic would apply even to accelerating frames in the absence of gravity.)

 

[yuiop]

I'm afraid that doesn't really make sense. The only frequency a photon has is the frequency an observer measures with a clock. Different observers measure different frequencies, so to say "the frequency stays the same" is wrong if two observers measure different frequencies at different heights. Frequency is an observer-dependent concept, as are time, distance, energy, etc. If two different inertial observers measure different energies there's no need to explain where the energy has gone because they are measuring in different frames.

I am talking more about the intrinsic physical frequency or energy of the photon. I agree that observers at different heights would measure different frequencies and that is the conventional view but I am looking deeper than that, as I always like to get a feel for what is really physically happening by deduction and logic. Meaurements often involve calculations rather than being direct measurements. For example when we measure velocity we measure the distance and record the elapsed time to cover that distance and then divide the distance by time. To measure distance we require two spatially separated observers and two clocks. In a gravitational field the two clocks at either end of a vertically orientated ruler are running at different rates. If we calculate the distance by timeing how long it takes a light signal to travel from the top of the ruler (point A) to the bottom of the ruler (point B) we need a start time at A and a finish time at point B. It is not sensible to make a measurement with two clocks running at different rates, so we should choose one clock as the master clock and synchronise the other clock by speeding it up or slowing it down so that they both run at the same rate. For example observer A could set his clock to send a test signal at one second intervals down to observer B. Observer B could speed up his clock so that the signals from A arrive at one second intervals according to (speeded up) clock B. Observer B could also send signals up to A at one second intervals (on his speeded up clock) and A could confirm the signals are arriving at one second intervals. The two clocks are now synchronised and a sensible measurement of distance and velocity can now be made. With this arrangement it would be confirmed that the speed of light is slower, lower down in the gravitational field (as predicted by the Schwarzschild metric) and that the frequency of light does not really change as it moves vertically in a gravitational field. We KNOW clocks run at different rates at different heights, so it is a very blinkered approach to ignore that FACT when comparing other measurements at different heights that have a time component.

And if you choose to measure a rising photon at two different heights in a single accelerating frame, the photon's loss of energy (gravitational red-shift) is accounted for as a gain in potential energy. (That logic would apply even to accelerating frames in the absence of gravity.)

Potential energy in the gravitational context is a Newtonian concept. In GR, the concept of a rising photon giving up its energy to be stored as potential energy in a classical gravitational field is very questionable. See this discussion by Baez: http://math.ucr.edu/home/baez/physics/Relativity/GR/energy_gr.html


Here is something else to consider. I shine a household torch at a black hole for a few seconds. The photons from the torch are blue shifted as they fall towards the black hole and the frequency of the photons goes to infinity as they approach the event horizon of the black hole. Have really added infinite energy to the black hole by shining a torch at it for a few seconds? I think not. It seems more likely that if the torch emitted one Joule of energy, then the black hole eventually absorbs one Joule of energy. Therefore the energy of a photon does not change as it falls. Although GR can use many coordinate systems and in some of them it appears that energy is not conserved, it seems that we can always find a coordinate system where energy is conserved. That is something that is worth bearing in mind when you get junk mail offering to sell you a machine for $10,000 that will produce infinite free energy "as proven by General Relativity".

 

[sylas]

I am talking more about the intrinsic physical frequency or energy of the photon. I agree that observers at different heights would measure different frequencies and that is the conventional view but I am looking deeper than that, as I always like to get a feel for what is really physically happening by deduction and logic.

A photon really does not have any intrinsic physical frequency. Its frequency is relative to an observer; always. There's nothing else.

Here's a thought experiment for you. How could you tell whether or not *we* are all inside a large cavity, within a very large massive object? Can you use any "intrinsic" properties of photons to recognize that they are all blueshifted, down here in the hole in the middle of a super-planet?

The reality is -- you can't tell. There's nothing intrinsic about the frequency of a photon that let's you tell whether you are observing it at the bottom of a gravitational well, or outside the well. The redshift or blueshift is always and only a comparison of two observers; not an intrinsic property of a photon.

Cheers -- sylas

 

[DrGreg]

I am talking more about the intrinsic physical frequency or energy of the photon. I agree that observers at different heights would measure different frequencies and that is the conventional view but I am looking deeper than that, as I always like to get a feel for what is really physically happening by deduction and logic.

But you are just arbitrarily choosing one observer as your reference observer and then transforming other observations to the local frame of the reference observer. You're entitled to do this, but I'm entitled to choose another observer as my reference and come to a different conclusion.

If you're looking for some frame-invariant notion of frequency, the only answer is zero, which doesn't help much. (Zero because it's proportional to energy; the "rest energy" of a photon is proportional to its "rest mass" which is zero. Or just let v \rightarrow c in the Doppler shift formula.)

Potential energy in the gravitational context is a Newtonian concept. In GR, the concept of a rising photon giving up its energy to be stored as potential energy in a classical gravitational field is very questionable. See this discussion by Baez: http://math.ucr.edu/home/baez/physics/Relativity/GR/energy_gr.html

In general, energy is a problem in GR. I'm no expert in this, but I understand that in some specific circumstances it is nevertheless possible to come up with a sensible definition of energy that is conserved. The link that you provided includes these words:

"In certain special cases, energy conservation works out with fewer caveats. The two main examples are static spacetimes and asymptotically flat spacetimes."

"The Schwarzschild metric is both static and asymptotically flat, and energy conservation holds without major pitfalls."​

I haven't just made up potential energy in GR. In Schwarzschild coordinates it is, for a hovering object,

\frac{mc^2}{\sqrt{1 - 2GM/rc^2}}​

See Woodhouse, N M J (2007), General Relativity, Springer, London, ISBN 978-1-84628-486-1, pp. 100-101.

Here is something else to consider. I shine a household torch at a black hole for a few seconds. The photons from the torch are blue shifted as they fall towards the black hole and the frequency of the photons goes to infinity as they approach the event horizon of the black hole. Have really added infinite energy to the black hole by shining a torch at it for a few seconds?

No, because, in the frame of a distant hovering observer the photons would also lose an infinite amount of potential energy as they fell (taking an infinite time to do so). (Other frames would disagree, as energy is a frame-dependent concept.)

 

[valdar]

Here is something else to consider. I shine a household torch at a black hole for a few seconds. The photons from the torch are blue shifted as they fall towards the black hole and the frequency of the photons goes to infinity as they approach the event horizon of the black hole. Have really added infinite energy to the black hole by shining a torch at it for a few seconds?

If you shine the torch from deep space (no gravity around you) then yes that is what happens.

However, if you are standing on Earth and you do that, the photons would first be RED shifted as they leave Earth (Earths gravity is pulling it back)... then once they leave Earths gravity well there is no shift. When the light hits the black holes gravity well then there would be a blue shift.
This would be visible to ALL observers, its the interaction of light and gravity isn't it?

 

[yuiop]

I haven't just made up potential energy in GR. In Schwarzschild coordinates it is, for a hovering object,

\frac{mc^2}{\sqrt{1 - 2GM/rc^2}}​

See Woodhouse, N M J (2007), General Relativity, Springer, London, ISBN 978-1-84628-486-1, pp. 100-101.

There is somethng wrong with that equation. Is there a missing minus sign or should it be

{mc^2}*{\sqrt{1 - 2GM/rc^2}} ?​

As it stands, the equation you have posted suggests the potential energy is lowest at infinity. That is the exact opposite of Newtonian gravitational potential energy. Perhaps you could quote some of the text from Woodhouse to put the equation in context?

No, because, in the frame of a distant hovering observer the photons would also lose an infinite amount of potential energy as they fell (taking an infinite time to do so). (Other frames would disagree, as energy is a frame-dependent concept.)

The small "m" in the equation you posted is rest mass. A photon does not have rest mass so either a photon always has zero potential energy or that equation does not apply to photons. Can you show an equation that applies to photons seeing as that is what were talking about? Without that, your claim that a photon loses infinite potential energy (and donates inifinite energy to a black hole?) is unsupported.

"In certain special cases, energy conservation works out with fewer caveats. The two main examples are static spacetimes and asymptotically flat spacetimes."

"The Schwarzschild metric is both static and asymptotically flat, and energy conservation holds without major pitfalls."​

Fine words, but can someone demonstrate that energy is conserved with a numerical example? For example let us take a one kilogram mass that is stationary at infinity and let it fall to say a radius of 4GM/c^2. Can someone show a complete energy balance taking the terminal velocity, kinetic energy, momentum energy and potential energy into account such that energy is conserved?

(Use units such that c=1, m=1, G=1 and assume the mass of the black hole (M) =1000m)


This equation might be useful although I am not sure if it applies in a gravitational field:

Total energy = \sqrt{p^2c^2+m^2c^4}


where p = \gamma mv

and \gamma = \frac{1}{\sqrt{1-v^2/c^2}}

 

[DrGreg]

kev, you are right, there is something wrong with my last post.

First, I mistyped Woodhouse's formula, which is actually

\sqrt{1-2M/r}​

for the PE of a unit mass (in geometrised units). Clearly there is a problem applying that to a zero mass.

I will go away and have a deeper think about this. When I've collected my thoughts I will probably start a new thread about gravitational PE in GR, as we are straying from this thread's topic.

In the meantime, take a look at http://people.maths.ox.ac.uk/~nwoodh/gr/index.html , on which his later book was closely based. Lecture 12, Section 12.2 (pages 54-55), is the relevant section I was quoting.

 

[yuiop]

kev, you are right, there is something wrong with my last post.

First, I mistyped Woodhouse's formula, which is actually

\sqrt{1-2M/r}​

for the PE of a unit mass (in geometrised units). Clearly there is a problem applying that to a zero mass.

I will go away and have a deeper think about this. When I've collected my thoughts I will probably start a new thread about gravitational PE in GR, as we are straying from this thread's topic.

Cheers, I look forward to the new thread. Exploring PE in some more detail will be interesting.

If you shine the torch from deep space (no gravity around you) then yes that is what happens.

However, if you are standing on Earth and you do that, the photons would first be RED shifted as they leave Earth (Earths gravity is pulling it back)... then once they leave Earths gravity well there is no shift. When the light hits the black holes gravity well then there would be a blue shift.

Essentially correct (using unsynchronised clocks). The red shift leaving Earth will be microscopic compared to the blue shift that approaches infinite as the photon approaches the event horizon of the BH.

A photon really does not have any intrinsic physical frequency. Its frequency is relative to an observer; always. There's nothing else.

Here's a thought experiment for you. How could you tell whether or not *we* are all inside a large cavity, within a very large massive object? Can you use any "intrinsic" properties of photons to recognize that they are all blueshifted, down here in the hole in the middle of a super-planet?

The reality is -- you can't tell. There's nothing intrinsic about the frequency of a photon that let's you tell whether you are observing it at the bottom of a gravitational well, or outside the well. The redshift or blueshift is always and only a comparison of two observers; not an intrinsic property of a photon.

Cheers -- sylas

I agree that in the cavity you would not measure any intrinsic redshift or blueshift. I was talking about relative measurements between two different observers at different potentials and intelligently interpreting the result to draw valid conclusions. I will post more tomorrow on time time dialtion and photon frequency when I have more time.

 

[yuiop]

An extended thought experiment to illustrate some interesting aspects of gravitational time dilation and photon frequency.

A ring is constructed around a black hole. It has a very large radius and is centred on the black hole. A smaller secondary ring is constructed with a radius a little larger that the event horizon of the black hole. One observer (A) is placed on the larger ring and a second observer (B) is placed on the smaller ring. Each observer has a standard clock, a small standard ruler, a long tape measure, a light signalling device and an ideal fibre optic cable. They each measure the local speed of light using their ruler and clock and note that the local speed of light is c (299,792,458 m/s). They each measure the circumference of their respective rings and time how long it takes a light signal to circumnavigate the ring inside an ideal fibre optic cable layed along the ring and note that the circumference of ring as measured by the tape measure is consistent with the circumference of the ring as calculated by timing how long it takes a light signal to go around. In other words nothing unusual is noted. A vertical ladder is constructed joining the two rings. A third observer (C)with their own standard clock and ruler checks the measuring devices against those of observer A to make sure they are correctly calibrated and then descends very slowly down the ladder and compares the transported clock and ruler against those of observer B. Again nothing unusual is noted. According to observer C the clocks of A and B are running at the same rate using C's direct local comparison method.

The initial conclusions from the measurements taken so far are:

Gravity has no effect on clocks.
Gravity has no effect on rulers.
Gravity has no effect on the speed of light.

These initial conclusions are naive and it appears that nothing interesting happens. The project funder is furious. He has spent millions on this experiment and this is the best this bunch of idiots can come up with? He issues further instructions. First they compare of the frequency of signals sent up and down and confirm that the frequency appears to change according to the gravitational gamma factor \gamma. Next they send signals up and down at one second intervals and conclude that the lower clock is running slower by a factor of y relative to the higher clock. They speed up the lower clock so that it is synchronised with the higher clock and now note that the speed of light horizontally is slower by a factor of y relative to the speed of light higher up. They measure the vertical distance of the connecting ladder using a rulers layed end to end and note that the measured vertical distance is a lot longer than would be assumed by calculating the distance using r = circumference/2/pi. Detailed examination reveals that rulers orientated vertically length contract by a factor of \gamma also.

When they piece all the information together the final conclusions are:

Lower clocks slow by a factor of \gamma relative to clocks higher up.
Lower vertical rulers contract by a factor of \gamma. relative to rulers higher up.
Horizontal rulers do not length contract.
The horizontal speed of light is slower by a factor of \gamma relative to the speed higher up.
The vertical speed of light is slower by a factor of \gamma^2 relative to the speed higher up.
The relative frequency of light does not change as photons rise or fall.
The energy of a photon relative to a photon higher up is constant.
The relative wavelength of light lower down is shorter by a factor of \gamma relative to light higher up.

They note that the equation c = wavelength*frequency still holds but in a gravitational field it is frequency that is constant and not the speed of light c when considered in a relative way.

Relative length, relative time and the relative speed of light all tend to zero as the event horizon is approached. Indeed it can be shown that photons hover at the event horizon. See: http://www.mathpages.com/rr/s7-03/7-03.htm

 

[JesseM]

A vertical ladder is constructed joining the two rings. A third observer (C)with their own standard clock and ruler checks the measuring devices against those of observer A to make sure they are correctly calibrated and then descends very slowly down the ladder and compares the transported clock and ruler against those of observer B. Again nothing unusual is noted. According to observer C the clocks of A and B are running at the same rate using C's direct local comparison method.

If this third observer were to synchronize his clock with A, descend slowly down the ladder, stay with B for a while and then slowly acend back up the ladder, he would note that his clock had fallen behind A's, so he'd know that some form of time dilation was taking place even if locally his clock always matched the rate of whoever he was next to at that moment.

Relative length, relative time and the relative speed of light all tend to zero as the event horizon is approached.

Only if by "relative" you mean "relative to the Schwarzschild coordinate system", which in GR is just one of an infinite number of equally valid coordinate systems for dealing with a black hole spacetime. One could also presumably come up with a coordinate system where "relative length, relative time and the relative speed of light all tend to zero" as you approach some radius from the center of the Earth--in both cases these statements have no deep physical significance, they are just an artifact of a particular choice of coordinate system.

Indeed it can be shown that photons hover at the event horizon. See: http://www.mathpages.com/rr/s7-03/7-03.htm

What that page is saying is that if a photon is directed outward in a radial direction by an event exactly on the event horizon, then the photon will hover there (in Kruskal-Szekeres coordinates its diagonal worldline would coincide with the diagonal representing the event horizon in these coordinates). It is certainly not saying that photons in general hover at the horizon, a photon moving inward will cross it just fine.

 

[rosie]

I'm puzzled by gravity - let alone time dilation. Stuck at first base. How is it that I can take two tennis balls - fill the one with rocks and drop them both down a tube, say, so no extraneous forces - then they both land at the same time? Yet picking up the one is more difficult than the other? More confusing yet - the one will bounce the other wont.

If gravity causes the initial drop - what comes into the equation that gives either of these balls the property of weight?

 

[yuiop]

I'm puzzled by gravity - let alone time dilation. Stuck at first base. How is it that I can take two tennis balls - fill the one with rocks and drop them both down a tube, say, so no extraneous forces - then they both land at the same time? Yet picking up the one is more difficult than the other? More confusing yet - the one will bounce the other wont.

If gravity causes the initial drop - what comes into the equation that gives either of these balls the property of weight?

Hi Rosie,

It is an interesting question, but it is slightly sidetracking the theme of this thread. Perhaps it is best if you post your question as new thread and I (and hopefully others) will have shot at answering it ;)

 

[yuiop]

What that page is saying is that if a photon is directed outward in a radial direction by an event exactly on the event horizon, then the photon will hover there (in Kruskal-Szekeres coordinates its diagonal worldline would coincide with the diagonal representing the event horizon in these coordinates). It is certainly not saying that photons in general hover at the horizon, a photon moving inward will cross it just fine.

For any radius > 2m the vertical coordinate speed of light is exactly the same whether the photons are going up or down. Only the direction sign changes but the magnitude is the same. Why is it that at the event horizon an outwardly emitted photon has zero velocity and inwardly emmited photon heads off to the central singularity? Clearly the magnitude of the velocity of the up and down photons is now different. Why is that? Why is it, that if I am below the event horizon and shine a torch downwards the photons travel forward in time to the central singularity and if I shine the torch upwards the photons still head towards the central singularity but this time they go backwards in time? Can I really make a photon go backwards in time just by changing the orientation of my torch? What is about the equation for the coordinate velocity of light that says the light emitted upwards from below the EH goes backwards in time and towards the central singularity, rather than forwards in time and away from the central singularity? I don't see anything there. It seems to be just an arbitary interpretation. When we look at the equation for motion of a massive particle in proper time the direction of motion is clearly indicated by the direction of advancing proper time and the equation clearly shows that a massive particle can leave the central singularity and head upwards towards the event horizon. Why can a particle with mass head up towards the event horizon and a photon can not? I would have put my money on the photon being the most likely to overcome gravity due to its higher velocity.

 

[JesseM]

For any radius > 2m the vertical coordinate speed of light is exactly the same whether the photons are going up or down.

Perhaps this is true in Schwarzschild coordinates, but it wouldn't be true in some other coordinate systems like Eddington-Finkelstein coordinates, for example. In any case, coordinate speeds are not important, the issue being discussed by that page is the actual physical behavior of photons--photons directed outward from events on the event horizon stay on the horizon forever, other photons do not.

Clearly the magnitude of the velocity of the up and down photons is now different. Why is that?

Different in what coordinate system?

Why is it, that if I am below the event horizon and shine a torch downwards the photons travel forward in time to the central singularity and if I shine the torch upwards the photons still head towards the central singularity but this time they go backwards in time?

They don't go "backwards in time" in any physical sense, they just go backwards relative to the time coordinate of Schwarzschild coordinates, which physically is not even timelike inside the horizon. Do you understand that the question of whether a given worldline is timelike or spacelike has a coordinate-independent answer, and that a line of constant t coordinate in Schwarzschild coordinates is spacelike outside the horizon but timelike inside, while a line of constant radial coordinate in Schwarzschild coordinates is timelike outside but spacelike inside? This is why if you want to talk about what happens inside the horizon you'll get yourself much less confused if you use Kruskal-Szekeres coordinates, where the vertical time axis is always timelike, and any timelike worldline will be closer to the vertical than a 45-degree light ray (all light rays are 45 degree straight lines in Kruskal-Szekeres coordinates) at every point, both outside and inside the horizon. Compare the timelike worldline A - A' - A'' in both Schwarzschild and Kruskal-Szekeres coordinates, in this diagram from the Misner-Thorne-Wheeler Gravitation textbook (p. 835):

Can I really make a photon go backwards in time just by changing the orientation of my torch? What is about the equation for the coordinate velocity of light that says the light emitted upwards from below the EH goes backwards in time and towards the central singularity, rather than forwards in time and away from the central singularity? I don't see anything there. It seems to be just an arbitary interpretation.

We've been through this before, kev--once again, can you tell me yes or no if you accept the standard GR notion that there is a clear distinction between coordinate-independent geometric facts about spacetime and worldlines, as opposed to facts which are only true in a particular choice of coordinate system? Do you agree that only the first type of facts have any objective physical meaning, and that no special holy significance should be attributed to the quirks of the Schwarzschild coordinate system?

When we look at the equation for motion of a massive particle in proper time the direction of motion is clearly indicated by the direction of advancing proper time and the equation clearly shows that a massive particle can leave the central singularity and head upwards towards the event horizon.

What does "advancing proper time" mean? In theory you can parametrize proper time to advance in either direction relative to coordinate time (even in SR nothing is stopping you from having proper time decrease as coordinate time increases, since the laws of physics are time-symmetric it is only thermodynamics that sets a physical arrow of time), but geometrically physicists can show that the worldline A - A' outside the horizon in the linked diagram connects up smoothly to the worldine A' - A'' inside the horizon (so both represent sections of a single continuous worldline), and if you want to have proper time defined in such a way that proper time advances along with coordinate time in Schwarzschild coordinates outside the horizon, then to be consistent you must have proper time decrease with increasing coordinate time inside the horizon (and decrease with increasing radial coordinate, which is really the timelike coordinate inside the horizon). If you didn't do this, you'd have a weird situation where a single particle's proper time went from increasing as it approached the horizon to decreasing as soon as it passed it, which wouldn't make any sense if you wanted proper time to represent elapsed time on an actual physical clock accompanying the infalling object. This is of course much more clear if you look at the A - A' - A'' worldline as represented in Kruskal-Szekeres coordinates, which avoids the misleading aspects of Schwarzschild coordinates.

 

[yuiop]

Do you understand that the question of whether a given worldline is timelike or spacelike has a coordinate-independent answer,

Yes I do, and if the worldline is spacelike in Schwarzschild coordinates, then it is spacelike in Kruskal-Szekeres coordinates too.. precisely because it coordinate-independent.

and that a line of constant t coordinate in Schwarzschild coordinates is spacelike outside the horizon but timelike inside, while a line of constant radial coordinate in Schwarzschild coordinates is timelike outside but spacelike inside?

The proper time of a falling observer is always positive as it falls in Schwarzschild coordinates and this is true above or below the horizon. This means above and below the horizon the invariant interval is timelike, but since timelike become spacelike below the horizon in Schwarzschild coordinates then the motion of the falling observer is spacelike below the horizon and by definition the observer is exceeding the speed of light. Since the invariant interval of an infalling observer is spacelike below the horizon in Schwarzschild coordinates it follows that the motion of a falling observer is spacelike below the horizon in Kruskal-Szekeres coordinates too, because it is an independent invariant quantity as you keep mentioning.

(all light rays are 45 degree straight lines in Kruskal-Szekeres coordinates)

A light ray at 45 degrees in a coordinate system does not indicate which way the light is going and this is difficult to determine because the proper time of a photon is zero. Proving that the path of a falling particle is timelike by comparing it to the supposed path of a photon whose direction you have not proven, proves nothing.

We've been through this before, kev--once again, can you tell me yes or no if you accept the standard GR notion that there is a clear distinction between coordinate-independent geometric facts about spacetime and worldlines, as opposed to facts which are only true in a particular choice of coordinate system? Do you agree that only the first type of facts have any objective physical meaning, and that no special holy significance should be attributed to the quirks of the Schwarzschild coordinate system?

I don't atribute special holy significance to Schwarzschild coordinates but I do not think it is an unfortunate choice of coordinates as it often described. If something is coordinate-independent geometric fact in any given coordinate system then it true in any other coordinate system. Kruskal-Szekeres coordinates do not have any higher claim to the truth over the supposedly misguided Schwarzschild coordinates. They have equally valid.

I wonder why you attribute holy significance to the quirks of Kruskal-Szekeres coordinates?

What does "advancing proper time" mean?

It means nothing get younger, not even twins in relativity. In SR and GR, the proper time can slow down relative to another clock, but never reverse. None of the twins ever ends up younger than they started in any thought experiment.

In theory you can parametrize proper time to advance in either direction relative to coordinate time (even in SR nothing is stopping you from having proper time decrease as coordinate time increases,

From now on I am counting birthdays in parametrized proper time. ;)

.. and if you want to have proper time defined in such a way that proper time advances along with coordinate time in Schwarzschild coordinates outside the horizon, then to be consistent you must have proper time decrease with increasing coordinate time inside the horizon (and decrease with increasing radial coordinate, which is really the timelike coordinate inside the horizon). If you didn't do this, you'd have a weird situation where a single particle's proper time went from increasing as it approached the horizon to decreasing as soon as it passed it, which wouldn't make any sense if you wanted proper time to represent elapsed time on an actual physical clock accompanying the infalling object.

Yep, it does not make sense, if objects really do continue to fall below the horizon, but I agree that is the conventional wisdom.

Take a look at the attached world maps in various projections. The top chart of the first diagram shows a view of the globe (Orthographic azimuthal projection) from both sides and the blue lines represent the path of a polar orbiting satellite projected onto the surface of the earth. The lower chart of the first image is a Mercator type projection of the world map that flattens the globe into a flat rectangle. The satellite path is also shown on this projection. In the second image the Mercator projection is squeezed in the middle to produce an unusual but still still valid chart of the Earth. Notice the large white empty triangular spaces. There is no need to fill those empty spaces with a parallel virtual Earth to make the geodesics complete. All the information from any of the first two charts is present on this chart also. Now a further chart on the right is created by rotating the left part of the squeezed chart clockwise to form a Kruskal-like map of the Earth. Note that the blue satellite path which is a true geodesic path does not look smooth and continuous in the Kruskal-like map as it crosses from the East quadrant to the North quadrant and yet we know in reality it is. Note that in this Kruskal-like Earth map "proves" that what we normally think of as North-South in Australia is actually East-West!. "Northlike" has become "Eastlike" just as timelike becomes spacelike in Kruskal-Szekeres coordinates. Because we are familiar with the Earth chart we are not fooled and we know North does not become East by the use of an unusual chart and we demonstrate this by simply checking a compass. However, if we are using an unusually distorted coordinate system to study unfamiliar territory like a black hole, then the absurdities are not so obvious. An additional red line has been added to the Kruskal-like map that represents a smooth and continuous geodesic in the Kruskal-like chart but it does not take a lot of visualisation to see that it does not represent the natural inertial motion of anything real. The moral is that a smooth and continuous continuation of a path as it crosses a boundary in a particular distorted coordinate system is not proof by itself that the path is smooth and continuous in reality.

 

[JesseM]

Yes I do, and if the worldline is spacelike in Schwarzschild coordinates, then it is spacelike in Kruskal-Szekeres coordinates too.. precisely because it coordinate-independent.

And do you agree that the line A'-A'' in the diagram I posted above is timelike, not spacelike? Do you agree that a line of constant radial coordinate in Schwarzschild coordinates is timelike outside the horizon but spacelike inside, whereas a line of constant t-coordinate in Schwarzschild coordinates is spacelike outside the horizon but timelike inside? Finally, do you agree that a horizontal line of constant t coordinate in Kruskal coordinates is spacelike everywhere, and a vertical line in Kruskal coordinates is timelike everywhere? If you disagree with any of these you are simply confused, if you would actually do the math and check whether the line element ds^2 is positive or negative for a small increment on any of these lines, you'd see that all these statements are correct.

The proper time of a falling observer is always positive as it falls in Schwarzschild coordinates and this is true above or below the horizon.

What do you mean by "always positive"? You can set the zero point of proper time anywhere you like. Perhaps you mean that proper time is always increasing with the t coordinate in Schwarzschild coordinates, but in this case you are mistaken, as long as we adopt the convention that there are no "local maxima" of proper time along a given worldline (meaning no points on a worldline where if you go in either direction away from a given point, the proper time decreases from its value at that point) then if the proper time is increasing with the t coordinate outside the horizon, it must be decreasing with the t coordinate outside the horizon. The only way to have the proper time increase with t coordinate both inside and outside is to have such a "local maxima" on the object's worldline at the point it crosses the horizon (which is not represented in Schwarzschild coordinates, but geometrically it's a perfectly real point in the spacetime manifold, and it is represented in Kruskal-Szekeres coordinates).

This means above and below the horizon the invariant interval is timelike but since timelike become spacelike below the horizon in Schwarzschild coordinates then the motion of the falling observer is spacelike below the horizon and by definition the observer is exceeding the speed of light.

No, you're completely confused here. First of all, just talking about the "invariant interval" ds^2 is meaningless without specifying what path you're calculating the invariant interval along--are you talking about a short interval along the worldline of the infalling particle? If so, then if you find it's timelike then it is timelike, period, that's a coordinate-independent geometric fact and it has absolutely nothing to do with whether the t-coordinate of your chosen coordinate system is timelike or spacelike. You calculate the value of the ds^2 along a path by integrating the line element along that path; the line element at every point is in turn determined by the metric, which is what encapsulates the actual geometric curvature of the spacetime. You can use any arbitrary coordinate system you like, including one where the t coordinate becomes spacelike or whatever, but the metric is specifically adjusted to each possible coordinate system in such a way that the integral of ds^2 between two events along a given worldline will have the same value in every coordinate system, so that "path length" is a geometric fact which is independent of your choice of coordinate system. Since the integral of ds^2 along a given path must be the same in ever possible coordinate system, then whether ds^2 is positive or negative must also be the same in every possible coordinate system, and that is what determines whether the path is spacelike or timelike.

So the worldline is still timelike in the horizon, as I'm sure could be checked if you parametrized a path like A'-A'' in the diagram and then checked the value of the line element ds^2 for an infinitesimal variation in the parameter--it would have the same sign as the line element for an infinitesimal variation in the parameter for the path A-A' of the same particle outside the horizon. It is the line element, based on the metric, that tells you in a real geometric terms whether a worldline is spacelike or timelike--do you understand that this is the sole determinant of the geometry, that all other features of particular coordinate systems are irrelevant to the meaning of "spacelike" and "timelike"?

Here's the line element in Schwarzschild coordinates (copied from here):

ds^2 = (1 - \frac{2m}{r}) c^2 dt^2 - \frac{1}{(1 - \frac{2m}{r})} dr^2 - r^2 ( d\theta^2 + r^2 sin^2 \theta d\phi^2 )

If you like, free feel to verify that for an infinitesimal increment along a line parallel to the t axis (meaning dr, d-theta and d-phi are all zero but dt is nonzero), if the line is at a value of r where r>2m (outside the event horizon), ds^2 will be positive (meaning the increment is timelike in a geometric sense), but if the line is at a value of r where r<2m (inside the event horizon), ds^2 will be negative (meaning it's spacelike). Likewise you could look at an infinitesimal increment along a line parallel to the r axis and verify that outside the horizon it's negative but inside the horizon it's positive.

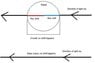
Incidentally, if you look at the diagram below, also from MTW's Gravitation, you can clearly see that the worldline of a particle lies inside the future light cone of events on its worldline both inside and outside the horizon, which is another way of thinking about the physical meaning of what it means for a worldline to be "timelike" (a physicist or mathematician could show that this definition is equivalent to the positive ds^2 notion, which is handy because in relativity light cones are very basic to the understanding of causality).

A light ray at 45 degrees in a coordinate system does not indicate which way the light is going and this is difficult to determine because the proper time of a photon is zero. Proving that the path of a falling particle is timelike by comparing it to the supposed path of a photon whose direction you have not proven, proves nothing.

Huh? I wasn't talking about the "direction" of a photon, and timelike vs. spacelike has nothing to do with the direction that proper time is increasing on a given path, it's only about the set of points in spacetime that the path passes through. Again, in GR it's always true that a path which remains inside the light cones (future or past) of every point along the path is a timelike one.

I don't atribute special holy significance to Schwarzschild coordinates but I do not think it is an unfortunate choice of coordinates as it often described. If something is coordinate-independent geometric fact in any given coordinate system then it true in any other coordinate system. Kruskal-Szekeres coordinates do not have any higher claim to the truth over the supposedly misguided Schwarzschild coordinates. They have equally valid.

I wonder why you attribute holy significance to the quirks of Kruskal-Szekeres coordinates?

Er, I don't. You don't seem to understand that timelike vs. spacelike is a geometric fact which is the same in all coordinate systems (once you've figured out the correct form of the metric in that coordinate system, you can use it to calculate the integral of ds^2 along a given path and your answer will be a coordinate-independent one), and that physicists have checked this already and verified that Kruskal-Szekeres happen to have the nice property that worldlines which are timelike in the coordinate-independent sense always have a slope closer to the vertical than 45 degrees when represented in these coordinates. Of course it's the geometry that's fundamental, but because of this "nice" property of Kruskal-Szekeres coordinates they are less likely to mislead you about the basic geometrical issues, as you have clearly been mislead by thinking about the "less nice" Schwarzschild coordinates.

It means nothing get younger, not even twins in relativity. In SR and GR, the proper time can slow down relative to another clock, but never reverse. None of the twins ever ends up younger than started in any thought experiment.

Then like I said, if you want to avoid a "local maxima" in proper time which would correspond to time decreasing in both directions from the maxima, you must define proper time in such a way that if proper time is increasing with Schwarzschild t coordinate on a given worldline outside the horizon, then it is decreasing with Schwarzschild t coordinate on the same worldline outside the horizon.

Yep, it does not make sense, if objects really do continue to fall below the horizon but I agree that is that conventional wisdom.

You're being a crackpot if you keep talking as though these issues are a matter of "conventional wisdom" as opposed to objectively right or wrong and probably not hard to check mathematically for anyone well-versed in GR.

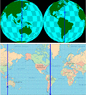
Take a look at the attached world maps in various projections. The top chart of the first diagram shows a view of the globe (Orthographic azimuthal projection) from both sides and the blue lines represent the path of a polar orbiting satellite projected onto the surface of the earth. The lower chart of the first image is a Mercator type projection of the world map that flattens the globe into a flat rectangle. The satellite path is also shown on this projection. In the second image the Mercator projection is squeezed in the middle to produce an unusual but still still valid chart of the Earth. Notice the large white empty triangular spaces. There is no need to fill those empty spaces with a parallel virtual Earth to make the geodesics complete.

As on a previous thread, you talk as though it's a matter of arbitrary fancy whether we think of different points in a coordinate map as being "the same" or "different", ignoring this thing called the metric which tells you how distances between points actually work in a geometric sense. The globe analogy is actually helpful in thinking about the meaning of the metric, though. Do you agree that on a globe, there is a geometric notion of distance along a given path, and that path with the shortest distance between any two points is a section of the great circle that contains both points? Do you agree that the apparent length of a given path in a given coordinate representation will not in general match up well with the actual geometric length? For example, if you have two horizontal lines of apparent equal length in a Mercator projection, one at the equator and one near the pole, they will not actually have equal geometric length if you map the corresponding points on the globe, the one at the equator will have a greater geometric length. Well, the metric in Mercator coordinates would tell you the line element at every point, and it would tell you that a given increment of the horizontal coordinate near the equator corresponds to a larger increment of ds^2 then the same sized increment of the horizontal coordinate near the pole, and if you integrated ds^2 along a path using the right formula for the line element in Mercator coordinates, you'd get back the actual geometric length of that path on the surface of the globe. And if you can calculate the coordinate-independent distance along all possible paths, then you can define how "nearby" an arbitrary pair of points are by looking at the length of the shortest possible path between them.

Even if the coordinate system does something weird like stretching out a single geometric point on the globe into a line in the coordinate representation (which is exactly what happens with the set of events at the event horizon in Schwarzschild coordinates), you could figure out that this set of different coordinate points is "really" a single geometric point by nothing that the shortest path between such points would have a geometric length of zero. Similarly, in the case of your triangular Earth diagram with empty white spaces, if you define the metric on each triangular slice and then identify points on the diagonals of each slice as in the right-hand version of your diagram, you could show geometrically using the metric on either slice that all the points along the diagonal are really a single geometric point (the North Pole). In GR I think defining what it means for different coordinate points to be the "same" geometrically would be a bit more complicated, since you can have lightlike paths between distinct points which have ds^2 = 0 along the path, but just from reading physicists talking about coordinate representations vs. geometry I'm sure that physicists and mathematicians do have some well-defined notion of what it means for points in spacetime with distinct coordinates to be the "same point" geometrically. And from reading physicists talk about the Kruskal diagram, they make clear that different points along the diagonal representing the event horizon actually are geometrically distinct points in the spacetime manifold, so this is unlike your triangular mapping of the Earth where all the points on the diagonal are really just the single geometric point of the North Pole, and thus the blue line can really be a single continuous line geometrically even though it appears to cross the diagonal at two different places.

 

[Max™]

They don't go "backwards in time" in any physical sense, they just go backwards relative to the time coordinate of Schwarzschild coordinates, which physically is not even timelike inside the horizon. Do you understand that the question of whether a given worldline is timelike or spacelike has a coordinate-independent answer, and that a line of constant t coordinate in Schwarzschild coordinates is spacelike outside the horizon but timelike inside, while a line of constant radial coordinate in Schwarzschild coordinates is timelike outside but spacelike inside? This is why if you want to talk about what happens inside the horizon you'll get yourself much less confused if you use Kruskal-Szekeres coordinates, where the vertical time axis is always timelike, and any timelike worldline will be closer to the vertical than a 45-degree light ray (all light rays are 45 degree straight lines in Kruskal-Szekeres coordinates) at every point, both outside and inside the horizon. Compare the timelike worldline A - A' - A'' in both Schwarzschild and Kruskal-Szekeres coordinates, in this diagram from the Misner-Thorne-Wheeler Gravitation textbook (p. 835):

Jesse is a smart guy, I was reading and thinking that something very obvious was missing, but couldn't figure out what it was, then it hit me that no one was considering the nature of the worldlines directly.

If you don't consider the worldlines themselves, you can do silly things like decree arbitrarily simultaneous timeslices to be universal for all observers, when they're obviously unique to each individual observer when compared against the worldlines themselves.


I always liked to say the degrees of freedom within a Schwarzschild hole are inwardly directed after being reversed. That isn't as clear as the above explanation though.

 

[A-wal]

I'm puzzled by gravity - let alone time dilation. Stuck at first base. How is it that I can take two tennis balls - fill the one with rocks and drop them both down a tube, say, so no extraneous forces - then they both land at the same time? Yet picking up the one is more difficult than the other? More confusing yet - the one will bounce the other wont.

If gravity causes the initial drop - what comes into the equation that gives either of these balls the property of weight?

I've said it before and I'll say it again:

1). It takes more energy to move an object which weighs more?

2). Because if it didn't work that way then if two objects were to touch in mid air then they would fall faster. If touching isn't enough then what difference would it make if they were properly joined?

3). Because objects in free fall aren't really falling?

The answer is 3. When an object is in free fall, it is in fact at rest. It's the ground that's moving up, which pushes anything on the surface down. Length contraction stops things from actually moving outwards.

Read my blogs. Then tell me what you thought. In fact I think they would be good to put in this section and made sticky, providing there's no errors of course. Technically they're not close to what real physicists could write but I think they'll be good for all the beginners that frequently come here.