Gravity Assist-Elliptical Trajectories

[rpthomps]

Good evening,

I am working my way through a JPL technical report I found online at

link

Specifically, I am at page 17 which looks like

and I am trying to understand the relation

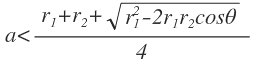
I basically, don't understand where this relationship comes from and why it is necessary.

Any help would be appreciated.

Ryan

 

[dauto]

Well, there is a mistake in that equation. There should be another term inside the square root. The missing term is (r₂)². That triangular inequality simply expresses that r₁' and r₂' must add to something larger than the distance between P₁ and P₂ which can be found from r₁, r₂, and θ by use of the law of cosines.

 

[rpthomps]

Thanks Dauto