karush
Gold Member
MHB
- 3,240
- 5
In the standard (x,y) coordinate plane below, 3 of the vertices of a rectangle are shown. Which of the following is the 4th vertex of the rectangle?
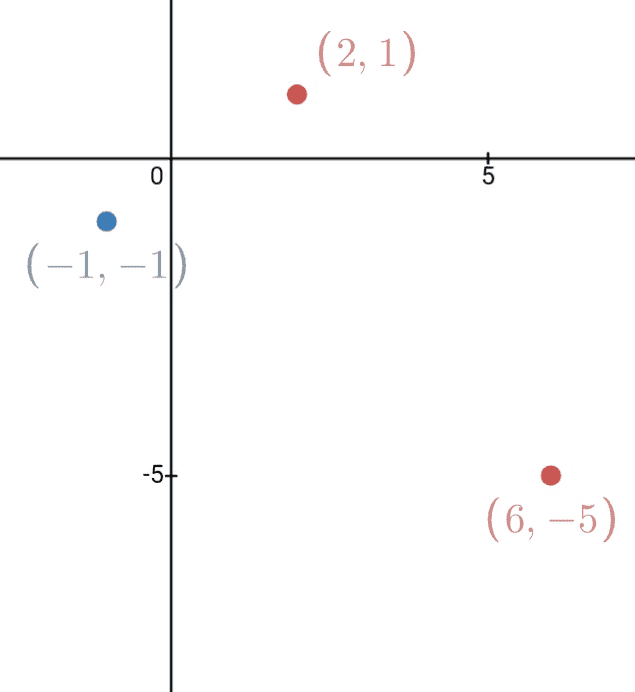
sorry about the huge image but couldn't find where to scale it down
a. (3,-7)
b. (4,-8)
c. (5,-1)
d. (8,-3)
e. (9,-3)
ok I don't think we need a bunch of equations to do this
$\delta$ x of the with is 3
$\delta$ y of the width is 2
so the fourth corner is
(6-3,-5-2)=(3,-7)
sorry about the huge image but couldn't find where to scale it down
a. (3,-7)
b. (4,-8)
c. (5,-1)
d. (8,-3)
e. (9,-3)
ok I don't think we need a bunch of equations to do this
$\delta$ x of the with is 3
$\delta$ y of the width is 2
so the fourth corner is
(6-3,-5-2)=(3,-7)