Pradhan34
- 5
- 0
I ran a search for gyroscopes looking for a definitive solution to the "What causes Precession?" and found no good clear answers. I think the Feynman lectures come close to the solution and followed that thought process, all the pieces point to the solution, I had to put my theory to the test on this forum. Please have some patience while reading this cause its long.
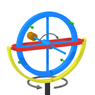
Feynman, From Lectures on Physics Volume 1 – “Rotation In Space”,talking about precession, quote “...When the wheel is precessing, the particles that are going around the wheel are not really moving in a plane because the wheel is precessing...the particles which are crossing through the precession axis are moving in curved paths, and this requires application of a lateral force. This is supplied by our pushing on the axle, which then communicates the force to the rim through the spokes... What about the particles that are going back on the other side...there must be a force in the opposite direction on that side. The net force we apply is zero.” The Visualization is given in first image from left attached below.
(This discussion is of precession of a bicyle wheel)
This quote was rather ambiguous and I resolved to see if 2D drawing of the precessing wheel did more justice. I drew it in Solidworks 2D drawing (Picture attached below –second from left below), and voila, a point precessing and also moving on the wheel does not move in a circle – but on a curve(each point(total 3) has it’s respective circle drawn – green, red, black – the black circle is the trace of the center of mass of the wheel, thus the point’s shadow lies on the center of mass at that point). To move along a circle an object needs centripetal force and a linear momentum (Without the linear momentum it isn’t going to move). But for a curve we need a centripetal force and a torque – the torque given by the coriolis force. When the wheel moves along the curve there must be a velocity, radial, moving the wheel element towards the center resulting in a coriolis force perpendicular to the radial velocity and being perpendicular provides the coriolis force a moment arm equal to the radius of the circle.
How does this result fit? In a demonstration of precession, we hold the string, spin up the wheel and release it. Nowhere do we give it the linear momentum it needs to go around the precession axis. The coriolis force provides just this torque, to push the wheel into the circular motion. While the centripetal force and its moment arm – the radius of the wheel (NOT THE PRECESSION RADIUS) - balances the torque due to gravity. Thus the torque due to gravity furnishes the centripetal force just as friction between car wheels and the road provide centripetal force to make a turn.
Now come the pitfalls,
This works really well for the top section. But reading the Feynman quote above –“ What about the particles that are going back on the other side...there must be a force in the opposite direction on that side. The net force we apply is zero.” So far we, think the torque due to gravity is a torque. But actually is a couple (the string tension and mg form a couple turning it clockwise ). So there must be a centripetal force 180 degrees to the one on the top. I can’t see it. I was hoping by placing this on the forum someone might figure it out.
If someone has a good apparatus, maybe you can do some rough calculations.
The coriolis force, the torque giving it linear momentum...fits too well to discard, I think i’m just not seeing it.
Then again I could be farting my *** off, twisting facts. So let me know, And thank you for reading this far. I could explain the coriolis force part in more detail if someone requires.
Feynman, From Lectures on Physics Volume 1 – “Rotation In Space”,talking about precession, quote “...When the wheel is precessing, the particles that are going around the wheel are not really moving in a plane because the wheel is precessing...the particles which are crossing through the precession axis are moving in curved paths, and this requires application of a lateral force. This is supplied by our pushing on the axle, which then communicates the force to the rim through the spokes... What about the particles that are going back on the other side...there must be a force in the opposite direction on that side. The net force we apply is zero.” The Visualization is given in first image from left attached below.
(This discussion is of precession of a bicyle wheel)
This quote was rather ambiguous and I resolved to see if 2D drawing of the precessing wheel did more justice. I drew it in Solidworks 2D drawing (Picture attached below –second from left below), and voila, a point precessing and also moving on the wheel does not move in a circle – but on a curve(each point(total 3) has it’s respective circle drawn – green, red, black – the black circle is the trace of the center of mass of the wheel, thus the point’s shadow lies on the center of mass at that point). To move along a circle an object needs centripetal force and a linear momentum (Without the linear momentum it isn’t going to move). But for a curve we need a centripetal force and a torque – the torque given by the coriolis force. When the wheel moves along the curve there must be a velocity, radial, moving the wheel element towards the center resulting in a coriolis force perpendicular to the radial velocity and being perpendicular provides the coriolis force a moment arm equal to the radius of the circle.
How does this result fit? In a demonstration of precession, we hold the string, spin up the wheel and release it. Nowhere do we give it the linear momentum it needs to go around the precession axis. The coriolis force provides just this torque, to push the wheel into the circular motion. While the centripetal force and its moment arm – the radius of the wheel (NOT THE PRECESSION RADIUS) - balances the torque due to gravity. Thus the torque due to gravity furnishes the centripetal force just as friction between car wheels and the road provide centripetal force to make a turn.
Now come the pitfalls,
This works really well for the top section. But reading the Feynman quote above –“ What about the particles that are going back on the other side...there must be a force in the opposite direction on that side. The net force we apply is zero.” So far we, think the torque due to gravity is a torque. But actually is a couple (the string tension and mg form a couple turning it clockwise ). So there must be a centripetal force 180 degrees to the one on the top. I can’t see it. I was hoping by placing this on the forum someone might figure it out.
If someone has a good apparatus, maybe you can do some rough calculations.
The coriolis force, the torque giving it linear momentum...fits too well to discard, I think i’m just not seeing it.
Then again I could be farting my *** off, twisting facts. So let me know, And thank you for reading this far. I could explain the coriolis force part in more detail if someone requires.