- #1
greypilgrim
- 508
- 36
Hi.
I'm trying to take a purely translational approach to precession (i.e. not using angular momentum and torque). I'm looking at a gyroscope that consists of four point masses on a cross and at a moment in time when one mass is at the topmost point (see sketch). I'm assuming a virtual translation of the center of mass caused by gravity (red arrow) and use energy conservation to compute the forces acting on the four masses (using basically the law of the lever). After some rather ugly calculations using lots of small-angle approximations I somehow managed to show that the forces on the upper and lower mass points (blue) cause precession and I found the correct value for its angular velocity.
However, there are still the forces acting on the two remaining mass points (green). How are they compensated?
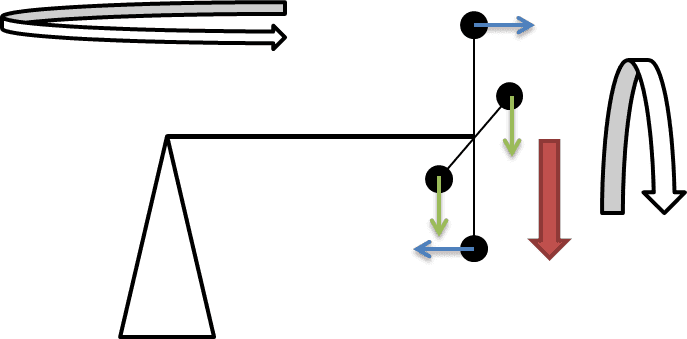
I'm trying to take a purely translational approach to precession (i.e. not using angular momentum and torque). I'm looking at a gyroscope that consists of four point masses on a cross and at a moment in time when one mass is at the topmost point (see sketch). I'm assuming a virtual translation of the center of mass caused by gravity (red arrow) and use energy conservation to compute the forces acting on the four masses (using basically the law of the lever). After some rather ugly calculations using lots of small-angle approximations I somehow managed to show that the forces on the upper and lower mass points (blue) cause precession and I found the correct value for its angular velocity.
However, there are still the forces acting on the two remaining mass points (green). How are they compensated?