HAT - Displacement of joint of the rods

[exuberant.me]

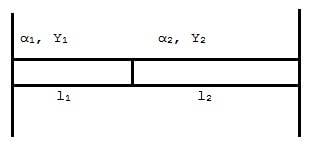
Two rods of different materials with coefficients of linear expansion α1 and α2 respectively; Young's moduli Y1 & Y2 respectively; of initial lengths l1 and l2 respectively are joined at one end. the free ends are fixed to two vertical walls as shown in the fig.
Temperature of the surrounding is then increased by T°C. Find out the displacement of the joint of the rods.

My work
Since my physics is not good so m not pretty sure about what i am applying..
but as i remember my friend guided me once to work on such questions..
I considered the displacement of the joint (say 'x') in any direction (right or left).
Now, x = Δl1 - Δl2 and,
k1Δl1 = k2Δl2
where, k = YA/L , "bulk modulous"
but the two eqns. only are not proving helpful.
If someone could guide me on this question.
Answer is.
x = l1l2(-Y1α1 + Y2α2) / (Y2l1 + Y1l2)

 

[Sunil Simha]

Assume that the rods cannot be compressed by other forces. So instead of a displacement in right or left direction, the rods will buckle (upwards). Now try solving it

 

[exuberant.me]

i need a soln.. couldn't get anything..!
at least give me the way to the eqns..!

 

[Sunil Simha]

Sorry exuberant.me,

The rules of Physics Forums don't allow users to give the solution to the questioner. However, we are allowed to give hints so the the questioner may develop the answer himself.

Also I'm sorry about the first post. I had not read the question properly.

When the rods reach an equilibrium (that is when they stop expanding) what can you say about the force on each other at the interface?

 

[Sunil Simha]

k1Δl1 = k2Δl2
where, k = YA/L , "bulk modulous"

I don't think this is right. The dimensions don't match.

 

[exuberant.me]

see the problem is "i have tried all i could" in this question..
so just guessing and reading the hints won't do..
According to me if a student has tried his hand to the fullest...
telling him 80% or the complete solution is of no harm...
After all i m preparing for my engineering examination and don't have good teachers here..
that is why i thought physics forum can help me someway... but unfortunately i have come to a wrong place..
sorry sir i don't need a soln. Thanks for your reply.. and thank you physics forum.

 

[haruspex]

Consider one rod in isolation, heated, and compressed by a force F. Obtain an expression for its change in length. Do the same for the other rod, same F. Writing that the total length does not change should give you three equations with three unknowns.

 

[exuberant.me]

okkay m writing set of eqns. and don't correct me as per the rules of physics forum
but just tell me which line is incorrect
1) F = k1Δl1 = (k1)(l1)(α1)T
2) F = k2Δl2 = -(k2)(l2)(α2)T
3) l = l1' + l2' = l1(1 + α1T) + l2(1 + (α2)T)
4) x = Δl1 - Δl2

 

[haruspex]

In your first eqn, you seem to have set the force so as to entirely compensate for the change in length due to temperature. If so, that won't give the right answer, since the two rods will need different forces. Pls try to follow the scheme I described.

 

[exuberant.me]

u have a point... seriously..!
see as i m poor in physics so please don't mind me posting something silly... thank u ...!
now u mean
F = k1Δl1 - k2Δl2 right..!
Also, l1' = l1 + x and l2' = l2 - x
so, l1' - l2' = (l1 - l2) + 2x
or, x = {(l1' - l1) - (l2' - l2)} / 2
something like this.. ?

 

[haruspex]

No. Just think about one rod. write an expression for its expansion, given the temperature change, and another for its compaction, given the force F. Then do the same for the other. What you know is that the sum of the two expansions equals the sum of the two compactions.

 

[exuberant.me]

See what i feel about the situation goes like this..
As the temperature increases, both the rods will expand. Since the length (l1 + l2) is fixed so they will oppose each others expansion.. ultimately resulting in the displacement of the joint.
Now let's say the displacement of the joint takes place in the right direction to a distance x.
So, for rod no. 1
it would expand to Δl1 but due to the opposite force by rod no. 2
k1x = k2(Δl1 - x) [Agreed??]
but i m having problem writing the eqn. for the other rod.
should it be k2x = k1Δl1 - k2Δl2
well my id is me.exuberant1@gmail.com :P

 

[exuberant.me]

i think this is the correct eqn.
(k1 + k2)x = k1Δl1 - k2Δl2
but on solving furthur i m getting
-ve of the answer.. am i correct at the same time as
i've considered the expansion towards right... !

 

[haruspex]

I have provided you, twice, with what I believe to be the simplest and clearest approach. By trying to consider the whole system in one go you keep confusing yourself. If you don't understand what I've suggested then say so.

 

[exuberant.me]

As u said,
consider one rod in isolation, heated, and compressed by a force F. Obtain an expression for its change in length.
Now my problem is what is should be the change in length...
i m trying to write the eqn. but u r not telling me its right or wrong...
like, Acc. to Me...
change in length = (l2 - x)
and,
change in length for the first rod = (l1 + x)
m not sure what F must be equal to..!
This is my problem.. hope u got it..!

 

[exuberant.me]

The first rod would have expanded to Δl1 but due to the opposite force it could expand only till x
so, F = k1(Δl1 - x)
for the other rod
it would have expanded to Δl2 but due to the opposing force...
F = k2(-Δl2 + x)
?

 

[haruspex]

1st rod, initial length l1, coefficient of linear expansion α1, heated by T degrees. For eqn see http://en.wikipedia.org/wiki/Thermal_expansion#Coefficient_of_thermal_expansion, the linear part.
What is the change in length?

1st rod, initial length l1, elastic modulus Y1, subjected to a compressive force F. Assume cross-sectional area is A (this should cancel out later). For eqn see http://en.wikipedia.org/wiki/Young's_modulus#Calculation. What is its change in length?

If both of the above are done, what is the total change in length?

 

[exuberant.me]

why r u giving me the link to the formulas? As if i don't knw them..!

just answer me by replying "right" or "wrong' ...

for rod 1
when it is stretched by a distance x
$F = \frac {Y_1Ax}{L}$
so change in length is,
l1' - l1 = x (because I've assumed that the joint gets displaced by x and not $\triangle l \ completely \ due \ to \ the \ opposing \ force \ by \ second \ rod$.)

Let's stop here...

now just tell me everything wrong that i have being written in my soln.
and i won't ask for ur furthur help...
nd thanks a lot for not getting irritated...!

 

[haruspex]

My first qn was in relation to the thermal expansion, but you've addressed the 2nd one:

for rod 1 when it is stretched by a distance x
$F = \frac {Y_1Ax}{L}$

The force compresses it, so the change in length will be negative. You need to rearrange the equation in the form: change in length due to force F = ΔL_F = (some function of F, Y, A, L).
For my first question, you need an eqn in the form:
change in length due to heating T = ΔL_T = (some function of T, σ, L).

so change in length is,
l1' - l1 = x (because I've assumed that the joint gets displaced by x

No, we're not ready to think about the displacement of the joint yet. We're dealing with changes to one rod in isolation, due to some force F and temperature change T - that's all.