Addem
- 20
- 0
Homework Statement
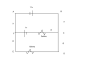
Linked below is a rough picture of the circuit for which I need to find the currents.
https://docs.google.com/drawings/pub?id=1jY6r1yjOf9OG5VixjZKcQbG2rj-ZQ7LZzaybGzkjva0&w=960&h=720
Homework Equations
Kichhoff's Laws, Ohm's Law.
The Attempt at a Solution
I'm doing a self-study using a book that I think may be riddled with errata, so I keep finding that I'm getting a result which disagrees with the answer the back and cannot see why my answer differs. I get the system of equations
11 - 3i_{3} + 1 = 0
11 + 6i_{2} = 0
-3i_{3} + 1 -6i_{2} = 0
i_{3}=i_{1}+i_{2}
I believe my choice of direction of flow is consistent and cannot affect my solution up to a change of sign. The book produces the result that i_{2}=13/6 when I obtain 11/6.