Schott11
- 3
- 0
I’m trying to understand the difference between how two styrofoam boxes of water cool when placed in a freezer.
see attachment for picture
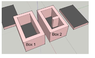
Both boxes are 6’’ wide, 10’’ long and 6’’ high.
Both boxes have an internal cavity of 4x8x4 (1 inch of insulation on all 6 sides)
Box 2 has an extra piece of wall that extends into the center of the cavity, it is 1 inch wide and 2 inches long.
The boxes are made out of styrofoam that has an R value of 5 / inch.
Assume the top fits air tight and each box is filled with water at 70°F, and placed in a freezer that is a constant 10°F.
The internal surface area (area in contact with water) of box 1 is 160 in2 or 1.111 ft2
The internal surface area of box 2 is 172 in2 or 1.1944 ft2
Using
Q / t = Area * (T-hot - T-cold) / thermal resistance (Rfactor)
I show that
Box 1 transfers 13.332 BTU/Hour
&
Box 2 transfers 14.333 BTU/Hour
My questions are:
How is it that Box 2 is transferring more heat, despite more insulation? Am I missing something in the setup?
If not, and Box 2 is cooling faster, what is happening at the extra wall that extends into the cavity of water in box 2? Is it conducting more heat because of the increased surface area?
Thanks
see attachment for picture
Both boxes are 6’’ wide, 10’’ long and 6’’ high.
Both boxes have an internal cavity of 4x8x4 (1 inch of insulation on all 6 sides)
Box 2 has an extra piece of wall that extends into the center of the cavity, it is 1 inch wide and 2 inches long.
The boxes are made out of styrofoam that has an R value of 5 / inch.
Assume the top fits air tight and each box is filled with water at 70°F, and placed in a freezer that is a constant 10°F.
The internal surface area (area in contact with water) of box 1 is 160 in2 or 1.111 ft2
The internal surface area of box 2 is 172 in2 or 1.1944 ft2
Using
Q / t = Area * (T-hot - T-cold) / thermal resistance (Rfactor)
I show that
Box 1 transfers 13.332 BTU/Hour
&
Box 2 transfers 14.333 BTU/Hour
My questions are:
How is it that Box 2 is transferring more heat, despite more insulation? Am I missing something in the setup?
If not, and Box 2 is cooling faster, what is happening at the extra wall that extends into the cavity of water in box 2? Is it conducting more heat because of the increased surface area?
Thanks