Heat transfer in a nuclear reactor and the electrical equivalent

[dRic2]

Homework Statement

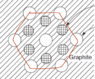
see picture below

Relevant Equations

heat transfer equation

To write the equation I took as the control volume the following block:

and the equation I wrote are:

$$ 6m_{f} c_{p_{f}} \frac {dT_{f}}{dt} = 6P - \frac 1 {R_1} (T_f - T_g) \text{ for the fuel}$$
$$ m_{g} c_{p_g} \frac {dT_{g}}{dt} = \frac 1 {R_1} (T_f - T_g) - \frac 1 {R_2} (T_g - T_c) \text{ for the graphite}$$
$$ 3m_{c} c_{p_c} \frac {dT_{c}}{dt} = \frac 1 {R_1} (T_g - T_c) - 3G c_{p_{c}} (T_{out} - T_{in}) \text{ for the coolant}$$

$P$ is the power produced by each fuel element. In stationary condition just drop the time derivative. I'm not totally sure about the last one though...

I have no clue on point b). Can someone give me a hint ?

Thanks Ric

 

[Astronuc]

Try drawing a triangular control boundary from the center of the central coolant channel to the center of two outer coolant channels, which has a fuel element in the middle. See the symmetry. The temperature is like the voltage, heat flux like the current through the fuel and graphite into the coolant. There are thermal resistances.

 

[dRic2]

Try drawing a triangular control boundary

If I take the triangular boundary the equations become:
$$ m_{f} c_{p_{f}} \frac {dT_{f}}{dt} = P - \frac 1 {R_1} (T_f - T_g) \text{ for the fuel}$$
$$ m_{g} c_{p_g} \frac {dT_{g}}{dt} = \frac 1 {R_1} (T_f - T_g) - \frac 1 {R_2} (T_g - T_c) \text{ for the graphite}$$
$$ m_{c} c_{p_c} \frac {dT_{c}}{dt} = \frac 1 {R_1} (T_g - T_c) - G c_{p_{c}} (T_{out} - T_{in}) \text{ for the coolant}$$
They are simpler (thanks for the suggestion ), but I don't think that my first try was wrong. In fact the mass of moderator inside the boundary in this case is less than what I considered in the previous post. At the end they should give the same result, correct ?

There are thermal resistances.

If the system is stationary I think I did it. I can re-arrange the last equation imposing $T_{c} = \frac {T_{in} + T_{out}} 2$ :

$$m_c c_{p_c} \frac {dT_c}{dt} = \frac 1 {R_1} (T_g - T_c) - 2G c_{p_{c}} (T_c - T_{in})$$

And the equivalent electrical network should be:

But in the general case there should be capacitors (the terms with $mc_p \frac{dT}{dt}$) and I don't know how to insert them properly inside the circuit. Maybe in parallel with the corresponding resistance ?

 

[Astronuc]

Since part a states "steady-state", then dT/dt = 0. The temperature gradients and heat flux should be constant. The heat leaving the fuel must equal the heat entering the coolant channel.

 

[dRic2]

Yes but I'd like to know the general case too, if it doesn't get too complicated. Anyway Thanks for the replies!