Height Ratio of A Coin below the Water

willydavidjr
Messages
66
Reaction score
0
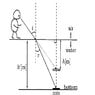
A coin is at the bottom of a pool with a depth of h^l[m]. The diagram I provided below shows the coin can appear to be in a place shallower than its actual depth.

Looking perpendicularly onto the water surface ( i\cong 0, r\cong 0 ), the coin looked as if it were in a place with depth h[m]. FInd the ratio of h^l/h of the two heights.

This is the site of the diagram: www.geocities.com/willydavidjr/coin ...
 

Attachments

  • coin.jpg
    coin.jpg
    18.1 KB · Views: 449
Last edited:
Physics news on Phys.org
Well, where's your solution? Apply Snell's law of refraction--and a bit of trig--and you can solve it. Hint: Consider small angles of incidence and refraction (close to the normal).
 

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Thread 'Please tell me where I am going wrong in this integral'

##|\Psi|^2=\frac{1}{\sqrt{\pi b^2}}\exp(\frac{-(x-x_0)^2}{b^2}).## ##\braket{x}=\frac{1}{\sqrt{\pi b^2}}\int_{-\infty}^{\infty}dx\,x\exp(-\frac{(x-x_0)^2}{b^2}).## ##y=x-x_0 \quad x=y+x_0 \quad dy=dx.## The boundaries remain infinite, I believe. ##\frac{1}{\sqrt{\pi b^2}}\int_{-\infty}^{\infty}dy(y+x_0)\exp(\frac{-y^2}{b^2}).## ##\frac{2}{\sqrt{\pi b^2}}\int_0^{\infty}dy\,y\exp(\frac{-y^2}{b^2})+\frac{2x_0}{\sqrt{\pi b^2}}\int_0^{\infty}dy\,\exp(-\frac{y^2}{b^2}).## I then resolved the two...
View full post »

Similar threads

I Calculating Water Pool Depth: Factors to Consider in Fluid Dynamics
Replies
13
Views
2K
Oscillation of free surface of water in parallelepiped container
Replies
13
Views
2K
Metallic coin over wooden block in glass of water - buoyancy
Replies
7
Views
2K
Optics question - coin at the bottom of a swimming pool
Replies
1
Views
5K
Force of water against a dam gate
Replies
29
Views
3K
Misunderstanding of Gravitational Potential Energy
Replies
7
Views
3K
Explaining Pressure & Depth Relationships in Fluids Using Halliday & Resnick
Replies
4
Views
2K
What is the Propagation Speed of Gravity Waves in Water?
Replies
3
Views
2K
Will the displacement of a solid ball affect the water level?
Replies
7
Views
2K
Change in Gravitational Potential Energy in Oscillating water mass
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top