I Help discretizing this PDE (stream function)

[Daniel Sellers]

TL;DR Summary

I have attempted two different methods of discretization for a PDE on a 2D annulus grid in cylindrical coordinates. I would appreciate anyone pointing out problems or suggesting better methods. This is part of research I am conducting as an undergrad.

I have a PDE that I want to solve for a stream function ψ(j,l) by discretizing it on a 2D annulus grid in cylindrical coordinates, then solving with guas-seidel methods (or maybe a different method, not the point):

(1/s)⋅(∂/∂s)[(s/ρ)(∂ψ/∂s)] + (1/s²)⋅(∂/∂Φ)[(1/ρ)(∂ψ/∂Φ)]

Where s and Φ are cylindrical coordinates, ρ is mass density (known through other means)

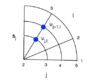
I've attempted to discretize this equation in a cell centered manner (which is what my professor suggested) but I also discretized it with ψ defined at the vertexes because it is easier for me to think about (I am fairly new to this type of numerical equation solving).

Vertex Centered Discretization (please see vertex centered grid attached):

(1/s_j)⋅(1/Δs²)⋅[(s_j+1/ρ_j+1,l){ψ_j+1,l - ψ_j,l} - (s_j-1/ρ_j-1,l){ψ_j,l - ψ_j-1,l}] + (1/s_j²)⋅(1/ΔΦ²)⋅[(1/ρ_j,l+1)⋅{ψ_j,l+1 - ψ_j,l} - (1/ρ_j,l-1)⋅{ψ_j,l - ψ_j,l-1}]

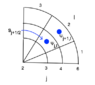
Cell Centered Discretization (see cell centered grid attached):

(1/s_j)⋅(1/Δs²)⋅[(s_j+3/2/ρ_j+1,l){ψ_j+1,l - ψ_j,l} - (s_j-1/2/ρ_j-1,l){ψ_j,l - ψ_j-1,l}] + (1/s_j+1/2²)⋅(1/ΔΦ²)⋅[(1/ρ_j+1,l)⋅{ψ_j,l+1 - ψ_j,l} - (1/ρ_j-1,l)⋅{ψ_j,l - ψ_j,l-1}]

In each case I am attempting to approximate the outside differential terms by finding difference in the slope of ψ at either end of Δs for each iteration.

Does this make sense to anyone familiar with this type of numerical problem solving? Are there any obvious flaws, instabilities or oversights I've missed?

 

[Daniel Sellers]

Oh, I should probably mention that I am only giving the terms which I need help discretizing. The rest of the equation is straightforward to discretize and is mostly constant terms.

 

[Chestermiller]

Shouldn't the mass density be constant? If not, please describe the exact problem being solved.

 

[Daniel Sellers]

No, the density depends on s and Φ, the entire equation is:

(1/s)⋅(∂/∂s)[(s/ρ)(∂ψ/∂s)] + (1/s2)⋅(∂/∂Φ)[(1/ρ)(∂ψ/∂Φ)] - 2Ω + ρ(c₀ + c₁ψ) = 0

Where Ω is frame rotation rate and c₀, c₁ are arbitrary constants (from the first and second term of a taylor expansion).

 

[Chestermiller]

$$\frac{1}{s}\frac{\partial}{\partial s}\left(\frac{s}{\rho}\frac{\partial \psi}{\partial s}\right)=\frac{1}{s_i}\frac{\left[\frac{s_{i+1/2}}{\rho_{i+1/2}}(\psi_{i+1,j}-\psi_{i,j})-\frac{s_{i-1/2}}{\rho_{i-1/2}}(\psi_{i,j}-\psi_{i-1,j})\right]}{(\Delta s)^2}$$