magnetics
- 47
- 0
Magnetic field lines around multipolar magnets get quite complex. There are local field vectors and field gradients in the x, y, & z plane. In the following diagrams I have tried to illustrate field lines around a centrally (half and half) charged disc magnet. The top diagram represents the field lines and the bottom the field gradients in the xy plane (assuming the xy plane in parallel to the surface and the z plane perpendicular).
I would love for learned PF magnetism experts to critique these illustrations. Thank you.
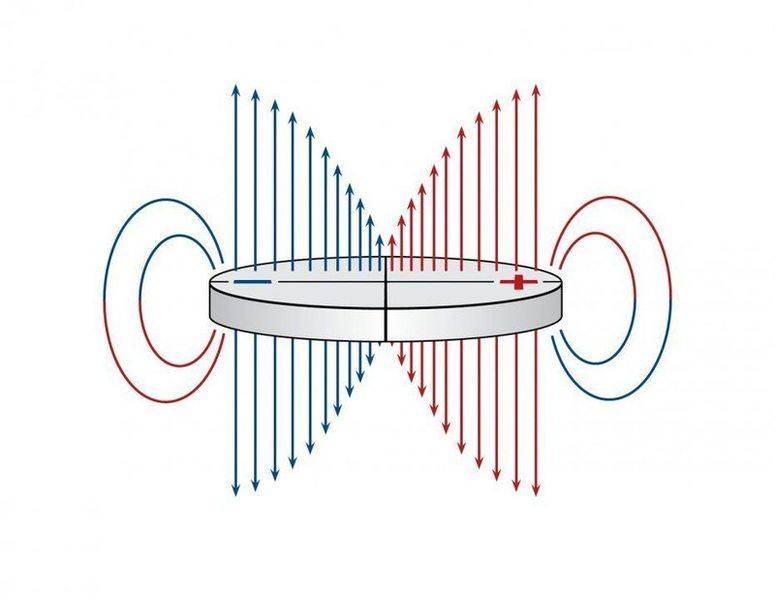
(I realize the colour of these field lines be swapped on the bottom)
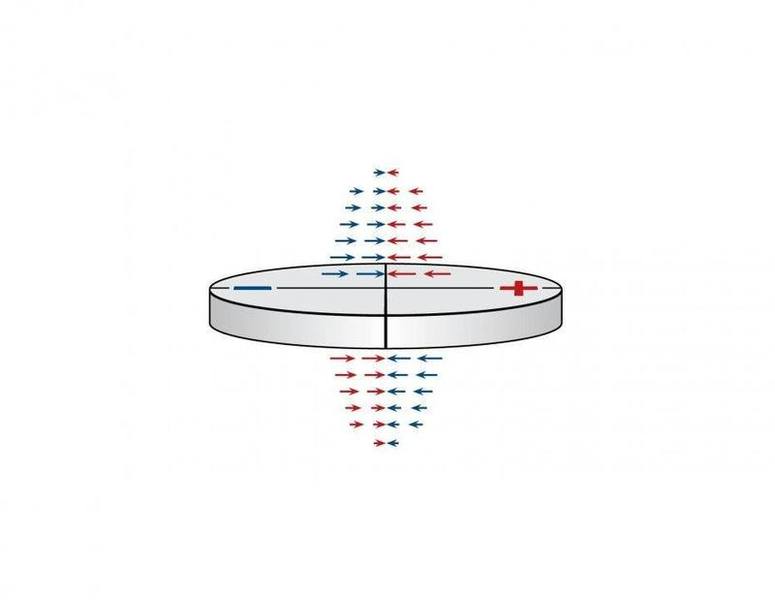
I would love for learned PF magnetism experts to critique these illustrations. Thank you.
(I realize the colour of these field lines be swapped on the bottom)