Help needed in sign of area element -- how do we take sign

[core1985]

Hello
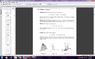
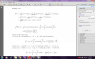
I just want to ask that in problem 1.54 why the sign of area element da is negative how do we predict signs in spherical coordinates unit vectors can anybody tell me the rule I have only trouble in sign like in left face it is negative what rule do we use for this negative sign

 

[vanhees71]

I think you do not look at the solution to the problem. While in the problem it's about Stokes's theorem, while the solution rather looks like an application of Gauss's theorem.

In Stokes's theorem you map a surface integral of the curl of a vector field to the line integral along its boundary. The surface and the boundary must be oriented positively relative to each other, i.e., such that when using the right-hand rule, when pointing with the fingers of your right hand in the direction of the boundary curve the thumb should point in the direction of the surface-normal element. Then for a vector field $\vec{V}$ you have
$$\int_{A} \mathrm{d}^2 \vec{F} \cdot (\vec{\nabla} \times \vec{V})=\int_{\partial A} \mathrm{d} \vec{r} \cdot \vec{V}.$$

In Gauss's theorem you have a volume $V$ is boundary $\partial V$. The surface normal vectors by definition always point out of the volume you integrate over. Then for a vector field $\vec{V}$ you have
$$\int_{V} \mathrm{d}^3 \vec{r} \vec{\nabla} \cdot \vec{V}=\int_{\partial V} \mathrm{d}^2 \vec{F} \cdot \vec{V}.$$
If you want more detailed answers to the specific problem, please post (with correct references/scans to the problem) in the homework forum!

 

[core1985]

No it is about checking divergence theorem I just want to know that should I consider this in left face of fig 1.48 that it is in theta and r and direction is - phi sue to it is place and here we shall take -y direction and that's why da = -dr r d theta (-ev phi direction)

 

[vanhees71]

So, it's about problem 1.53? Then you have to point the surface normal vectors out of the volume you integrate over. What I can see from the solution seems to be correct.