opus
Gold Member
- 717
- 131
This isn't a homework problem, but I was going to post it in there as my question is similar to one that would be asked there. However there doesn't seem to be a logic section for it so I posted it here.
The question is to make a logic table to determine if the following statement is valid:
Jane and Pete won't both win the math prize.
Pete will win either the math prize or the chemistry prize.
Jane will with the math prize.
Therefore, Pete will win the chemistry prize.
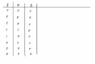
I've attached an image of my truth table, but I don't think it's correct as in none of the cases are all three of my premises true.
The question is to make a logic table to determine if the following statement is valid:
Jane and Pete won't both win the math prize.
Pete will win either the math prize or the chemistry prize.
Jane will with the math prize.
Therefore, Pete will win the chemistry prize.
I've attached an image of my truth table, but I don't think it's correct as in none of the cases are all three of my premises true.
Attachments
Last edited by a moderator: